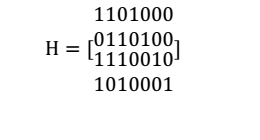線性分組編碼

背景

在通信中，由於信息碼元序列是一種隨機序列，接收端無法預知碼元的取值，也無法識別其中有無錯碼。所以在傳送端需要在信息碼元序列中增加一些差錯控制碼元，它們稱為監督碼元（校驗元）。這些監督碼元和信息碼元之間有確定的關係。

在信息碼元序列中加監督碼元就稱為差錯控制編碼，差錯控制編碼屬於信道編碼。

信息碼元和監督碼元之間有一種關係，關係不同，形成的碼類型也不同。可分為兩大類：分組碼和卷積碼。其中，分組碼是把信息碼元序列以每k個碼元分組，編碼器將每個信息組按照一定規律產生r個多餘的碼元（稱為校驗元），形成一個長為n=k+r的碼字。

當分組碼的信息碼元與監督碼元之間的關係為線性關係時（用線性方程組聯繫），這種分組碼就稱為線性分組碼。包括漢明碼和循環碼。

對於長度為n的二進制線性分組碼，它有種可能的碼字，從中可以選擇M=個碼字（k<n）組成一種編碼，其中碼字稱為許用碼字，其餘碼字稱為禁用碼字。這樣，一個k比特信息可以映射到一個長度為n的碼組中，該碼字是從M個碼字構成的碼字集合中選出來的，剩下的碼字即可以對這個分組碼進行檢錯或糾錯。

線上性分組碼中，兩個碼字對應位上數字不同的位數稱為碼字距離，簡稱距離，又稱漢明距離。

編碼中各個碼字間距離的最小值稱為最小碼距d，最小碼距是衡量碼組檢錯和糾錯能力的依據，其關係如下：

（1）為了檢測e個錯碼，則要求最小碼距d>e+1;

（2）為了糾正t個錯碼，則要求最小碼距d>2t+1;

（3）為了糾正t個錯碼，同時檢測e個錯碼，則要求最小碼距d>e+t+1,e>t。

線性分組碼是建立在代數群論基礎上的，各許用碼字的集合構成了代數學中的群，它們的主要性質如下：

（1）任意兩許用碼字之和（對於二進制碼這個和的含義是模二和）仍為一個需要碼字，也就是說，線性分組碼具有封閉性；

（2）碼字間的最小碼距等於非零碼的最小碼重。

由於碼字空間C是n維數二元線性空間中的一個k維子空間，由線性代數理論可知，

是由“1”或“0”元素組成的矩陣，它的k個行就是線性獨立矢量，，，。

矩陣G稱為線性碼C的生成矩陣。公式（1.1）建立了信息空間到碼字空間的線性映射。

經過行變換和列變換的矩陣生成的線性空間與原來的矩陣生成的線性空間是等價的，也就是說生成矩陣經過初等變換之後，所生成的碼與原來的碼是等價的。由此可以將生成矩陣經過變換之後，形成系統生成矩陣（即產生的碼中，信息碼元在碼字的高位部分，而校驗碼元在碼字的低位部分）。即

這也表示由G的行矢量所擴張成的k維子空間與H矩陣行矢量所擴張成的r維子空間是正交的。

G與H中只要有一個確定，另一個就是可以確定的。只要校驗矩陣給訂=定，校驗碼元和信息碼元之間的關係就完全確定了。


信息組　m₂m₁m₀	碼字