Gell-Mann矩陣實際就是上是SU(3)群特定選取的一組生成元(李代數)的特定基礎表示。所謂“特定選取”是指這些矩陣的正交性(至多差一個歸一化因子)。也就是說以這些特定矩陣為基的SU(3)伴隨表示是么正的。“特定基礎表示”是由於物理學家約定了一種常用的表示,而不是其他等價表示。Gell-Mann矩陣是為了分析強相互作用味對稱性而提出的(u,d,s夸克之間的SU(3)對稱性),廣泛套用於強子分類。而之後物理學家們在分析其他SU(3)對稱性時都會選取這種表示(比如色的SU(3)對稱性)。
基本介紹
- 中文名:Gell-Mann矩陣
- 外文名:Gell-Mann matrices
定義,性質,物理中的套用,發展歷史,
定義
在利用強相互作用SU(3)味對稱性進行強子分類時,Gell-Mann所提出的SU(3)群特定選取的一組生成元(李代數)的特定基礎表示,這種矩陣表示被稱為Gell-Mann矩陣。具體定義見圖1:

SU(3)的生成元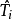 (基礎表示)定義為:
(基礎表示)定義為:
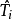

所謂“特定選取”是指矩陣 的正交性(至多差一個歸一化因子)。也就是說以這些特定矩陣為基的SU(3)伴隨表示是么正的。“特定基礎表示”是由於物理學家約定了一種常用的表示,而不是其他等價表示。
的正交性(至多差一個歸一化因子)。也就是說以這些特定矩陣為基的SU(3)伴隨表示是么正的。“特定基礎表示”是由於物理學家約定了一種常用的表示,而不是其他等價表示。

性質
在定義內積後,Gell-Mann矩陣具有正交性:

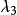




 圖2
圖2物理中的套用
Gell-Mann矩陣在強子分類中有重大意義,可以看見圖2中已經將u,d,s夸克及其對應的反夸克填入權圖之中。一方面,數學上是由於Gell-Mann矩陣建立時,就是選取在以u,d,s為基的SU(3)的基礎表示下;另一方面,我們也可以看出 和
和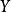 的物理意義。
的物理意義。

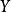
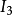


 圖3
圖3發展歷史
1961年蓋爾曼在奇異數守恆定律的基礎上,又提出了SU(3)對稱性。對強相互作用的粒子進一步作出分類。效仿佛教的“八正道”(即“正見、正思維、正語、正業、正命、正精進、正念、正定”),1962年蓋爾曼和以色列物理學家內曼(Y. Neemann)獨立地提出了“八正法”的分類方法。他們假設,八個質量最小的重子;兩個核子、三個Σ超子、兩個E超子及一個∧超子,構成一個“超多重態”。這八個重子,自旋都是1/2,宇稱均為正值,質量相近。只是電荷不同、同位旋不同、奇異數不同。因此可以畫一個超荷Y和同位旋分量I3的坐標圖,二重態、三重態和單態可以排成一個整齊的六邊形列陣。
蓋爾曼打算用八正方法把所有新的粒子和新的量子數都綜合進來。按照這一方法,還可以把當時已知的九個重子共振態排列成對稱的圖形。從這張圖形的對稱性考慮,似乎缺少了一個粒子,這個粒子的特性可以從圖形的對稱性推出。1962年蓋爾曼在歐洲核予研究中心的會議上提出這個失蹤的粒子應該具有電荷為一1,奇異數為一3,質量為1680兆電子伏,自旋為3/2,字稱為正值。1964年果然發現了Ω粒子正是這個失蹤的粒子。這樣就對蓋爾曼的八正方法作出了有力的支持。


