魔方矩陣又稱幻方,是有相同的行數和列數,並在每行每列、對角線上的和都相等的矩陣。魔方矩陣中的每個元素不能相同。你能構造任何大小(除了2x2)的魔方矩陣。
基本介紹
- 中文名:魔方矩陣
- 別稱:幻方
- 最早記錄於:我國古代的洛書
介紹
歷史
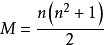
魔方構造
N 為奇數時
N為4的倍數時
N 為其它偶數時
算法設計
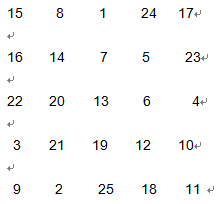
魔方函式
C語言版的魔方矩陣算法
// 交換void Exchange(int **pj, int tr, int tc, int n) { n++; if (1 <= tr && tr <= n / 2 && 1 <= tc && tc <= n) { pj[tr][tc] += pj[n - tr][n - tc]; pj[n - tr][n - tc] = pj[tr][tc] - pj[n - tr][n - tc]; pj[tr][tc] -= pj[n - tr][n - tc]; }}int main(){ int n, i = 0, j = 0, **pj; int tr, tc; printf("輸入魔方矩陣的階層:"); scanf("%d",&n); // 初始化二維數組 pj = (int**)malloc(sizeof(int **) * (n + 1)); for (i = 0; i < (n + 1); i++) pj[i] = (int*)malloc(sizeof(int *) * (n + 1)); // n為奇數時 if (n % 2 == 1) { // 1.將1放至第一行中間 i = 1; j = n / 2 + 1; pj[1][n / 2 + 1] = 1; // 2.沿右上45°,依次放置剩下的數 for (int k = 2; k <= n * n; k++) { // 行數上移,列數右移,即右上45°移動 tr = i - 1; tc = j + 1; // 條件一:若超出,則迴繞 if (tr < 1) tr = n; if (tc > n) tc = 1; // 條件二:若有數據,則放在上一個數字之下 if (0 < pj[tr][tc] && pj[tr][tc] <= n * n) { tr = i + 1; tc = j; if (tr < 0) tr = n; } pj[tr][tc] = k; i = tr; j = tc; } } // n為4的倍數時 else if (n % 4 == 0) { i = 1; j = 1; // 1.先將數據從上到下,從左到右填入 for (int k = 1; k <= n * n; k++) { pj[i][j++] = k; if (j > n) { j = 1; i++; } } // 2.將方陣的所有4*4子方陣中的兩對角線上的數 // 關於大方陣中心作中心對稱交換 i = 1; j = 1; for (size_t r = 0; r < n / 4 + 1; r++) { for (size_t c = 0; c < n / 4 + !(r % 2); c++) { tr = 2 * r + i; tc = 4 * c + r % 2 * 2 + j; Exchange(pj, tr, tc, n); Exchange(pj, tr - 1, tc, n); Exchange(pj, tr, tc - 1, n); Exchange(pj, tr - 1, tc - 1, n); } } } for (i = 1; i <= n; i++) { for (j = 1; j <= n; j++) printf("%d\t", pj[i][j]); printf("\n"); }}Java版的魔方矩陣算法
/***魔術矩陣,也被稱為魔方矩陣。目前魔術矩陣主要有三種結構:N為奇數、N為4的倍數、N為其它偶數(4n+2)。<br/>*其中目前很多數學家都還在研究“N為4的倍數”、“N為其它偶數(4n+2)”,可見它們對於初學者而言太難。<br/>*因此此處演示的代碼,僅僅考慮N為奇數的情況。<br/>*此代碼作為課件提供給學生參考,在學完數組、循環、判斷後練習。<br/>*@authorluo_wenqiang在126點com*@version1.0.0*/classMagicArray{publicstaticvoidmain(String[]args){/*1.把1放在第一行的最中間2.每個數字向右上角填充3.如果往右已經是最大數了,就從最左邊重新繼續4.如果往上已經是最大數了,就從最下邊重新繼續5.如果遇到行數的整數倍,則下一個數直接放到該數的下面*//*1.聲明一個n*n二維數組2.聲明一個int類型的變數記錄每個元素遞增的值,每次自加即可3.需要一個嵌套循環來填充二維數組3.1.把橫向的索引認為x,x=n/23.2.把縱向的所應認為y,y=03.3.在循環中,先把x、y坐標上的值填充,然後計算下一個坐標*/intn=3;int[][]array=newint[n][n];intcounter=1;//自加的計數器intx=n/2;inty=0;//二維數組,需要用兩層的嵌套循環來完成比較簡單for(inti=0;i<n*n;i++){//根據坐標填充值array[y][x]=counter;//計算下一個坐標的位置if(counter%n==0){//如果counter是n的整數倍,下一個坐標是在當前數字的下面y++;}else{x++;y--;if(y<0){//如果y超出範圍,把y設定成最大y=n-1;}if(x==n){//如果x超出範圍,把x設定成最小x=0;}}//使用完以後計數器需要自加counter++;}for(int[]row:array){for(inti:row){System.out.print(i);System.out.print("\t");}System.out.println();}}}
