基本介紹
矩陣
簡介
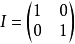


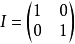

零矩陣,在數學中,特別是線上性代數中,零矩陣即所有元素皆為0的矩陣。在數學中,矩陣(Matrix)是一個按照長方陣列排列的複數或實數集合,最早來自於方程組的係數及...
矩陣的秩是線性代數中的一個概念。線上性代數中,一個矩陣A的列秩是A的線性獨立的縱列的極大數,通常表示為r(A),rk(A)或rank A。線上性代數中,一個矩陣A的...
列矩陣又稱列向量,是指有一列的矩陣。如果矩陣 A=(aij)m×n只有一行,即m=1,則此時稱之為行矩陣,或行向量。同樣,若 A=(aij)m×n只有一列,即n=1,這時...
半單矩陣(semisimple matrix)是一種特殊矩陣,指最小多項式無重根的矩陣。各種特殊的矩陣除半單矩陣外還有三角矩陣、冪零矩陣、冪等矩陣和冪麼矩陣等。半單矩陣...
若有一個矩陣滿足(1)是階梯形矩陣;(2)所有的非零行的第一個非零元素均為1,且其所在列中的其他元素都是零。 任何一個非零矩陣總可以經過有限次初等變換為...
矩陣範數(matrix norm)是數學中矩陣論、線性代數、泛函分析等領域中常見的基本概念,是將一定的矩陣空間建立為賦范向量空間時為矩陣裝備的範數。套用中常將有限維賦...
zeros功能是返回一個m×n×p×...的double類零矩陣。注意:m, n, p,...必須是非負整數,負整數將被當做0看待。當沒有參數時classname時,產生的是標量零...
只有對角線上有非0元素的矩陣稱為對角矩陣,或說若一個方陣除了主對角線上的元素外,其餘元素都等於零,則稱之為對角陣。...
《MATLAB零基礎入門教程(實例版)》是化學工業出版社出版圖書。...... 3.2.12 矩陣的轉置矩陣 563.2.13 矩陣的正交矩陣 573.2.14 矩陣的化零矩陣 57...
秩是線性代數術語,線上性代數中,一個矩陣A的列秩是 A的線性無關的縱列的極大數目。類似地,行秩是 A的線性無關的橫行的極大數目。矩陣的列秩和行秩總是相等...
線上性代數中,若爾當標準型(英語:Jordan normal form)或稱若爾當正規型(英語:Jordan canonical form)是某個線性映射在有限維向量空間上的特別的矩陣表達形式,稱作...
非平凡解是矩陣代數中的定義,屬高等數學內容。非平凡解是齊次方程或齊次方程組的非零解。...
線上性代數中,一個矩陣A的列秩是A的線性獨立的縱列的極大數目。類似地,行秩是A的線性獨立的橫行的極大數目。矩陣的列秩和行秩總是相等的,因此它們可以簡單地...
0 零售的邏輯編輯 鎖定 《零售的邏輯》是機械工業出版社2019年出版的圖書,分析...制定成功的零售戰略:卡恩零售成功矩陣 / 在卡恩零售成功矩陣上標繪零售商的競爭...
2.3.9矩陣元素的差分 482.4矩陣分析 492.4.1向量和矩陣的範數 492.4.2矩陣的秩 502.4.3矩陣的行列式 502.4.4矩陣的跡 512.4.5矩陣的化零矩陣 51...
