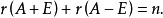半單矩陣

半單矩陣(semisimple matrix)是一種特殊矩陣，指最小多項式無重根的矩陣。各種特殊的矩陣除半單矩陣外還有三角矩陣、冪零矩陣、冪等矩陣和冪麼矩陣等。半單矩陣可以通過半單變換得到。

基本介紹

• 中文名：半單矩陣
• 外文名：semisimple matrix
• 定義：指最小多項式無重根的矩陣
• 類別：一種特殊矩陣
• 一級學科：數學
• 二級學科：矩陣

簡介

半單矩陣(semisimple matrix)是一種特殊矩陣，指最小多項式無重根的矩陣。與對角矩陣相似的n階矩陣A，存在n階可逆矩陣T，使TAT是對角矩陣。若A是數域P上的n階矩陣，且A的全部特徵值都屬於P，則A是半單矩陣的充分必要條件是：A的最小多項式無重根。復n階矩陣是半單矩陣的充分必要條件是：其最小多項式無重根。

半單變換

半單變換(semi-simple transformation)一類特殊的線性變換。設V是域P上的n維線性空間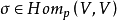，，若σ恰有n個線性無關的特徵向量，則稱σ為半單變換。半單變換關於基的矩陣是半單矩陣。線性變換σ為半單的充分必要條件是其最小多項式無重根。

相關特殊矩陣

三角矩陣

一種特殊矩陣。數域P上主對角線以下或以上的全體元素都是零的n階方陣：

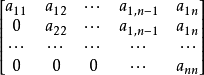
或

分別稱為上三角形矩陣和下三角形矩陣，亦稱上三角矩陣和下三角矩陣，統稱三角形矩陣。主對角元全是1的三角形矩陣稱為特殊三角形矩陣；主對角元全為零的三角形矩陣稱為嚴格三角形矩陣。兩個n階上（下）三角形矩陣的和、積以及P中的一個數與上（下）三角形矩陣的乘積仍是上（下）三角形矩陣。

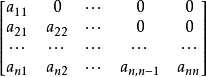
冪零矩陣

一種特殊矩陣。指冪零變換所對應的矩陣。亦即存在正整數m，使A^m=0的n階矩陣A。冪零矩陣是降秩矩陣。一個矩陣是冪零的充分必要條件是：它的特徵值全為零。若A^m=0，但A^m-1≠0，則E-A可逆，且

這時m稱為冪零矩陣A的冪零指數。

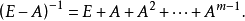
冪等矩陣

亦稱投影矩陣。一種特殊矩陣。指冪等變換所對應的矩陣。滿足A²=A的n階矩陣A稱為冪等矩陣。冪等矩陣或者是單位矩陣，或者是奇異的。如果A是冪等矩陣，則

式中r(A)是A的秩。

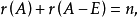
冪麼矩陣

一種特殊矩陣。指冪麼變換所對應的矩陣。即存在正整數m，使A^m=E的n階矩陣A。冪麼矩陣A是可逆的，且其逆矩陣為A^m-1；A的特徵值的模均為1。當m=2時，若有A²=E時，則A稱為對合矩陣，n階對合矩陣A的特徵值為1或-1，且