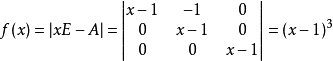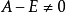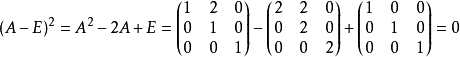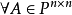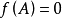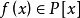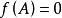最小多項式

最小多項式(minimal polynomial)是代數數論的基本概念之一。由Cayley-Hamilton定理，A的特徵多項式是A的零化多項式，而在A的零化多項式中，次數最低的首一多項式稱為A的最小多項式。

基本介紹

• 中文名：最小多項式
• 外文名：minimal polynomial
• 套用：矩陣的最小多項式
• 學科：數理科學
• 相關引理：Cayley-Hamilton定理
• 相關名詞：特徵多項式，零化多項式

定義

由Cayley-Hamilton定理， ， 是A的特徵多項式，則 。因此，對任一矩陣 ，總可以找到一個多項式 ，使 。此時，也稱多項式 以A為根。

設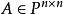 ，在數域P上的以A為根的多項式中，次數最低的首項係數為1的那個多項式，稱為A的最小多項式。

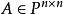
性質

①A的最小多項式是唯一的。

②設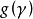是A的最小多項式，則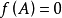等價於。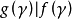

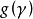
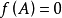
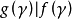
③A的最小多項式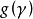是它的特徵多項式的一個因式。

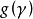
④A的最小多項式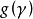與它的特徵多項式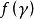在數域P中有相同的根。

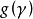
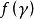
⑤相似的方陣陣具有相同的最小多項式。

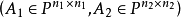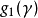⑥準對角矩陣的最小多項式等於的最小多項式與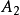的最小多項式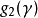的最低公倍數。

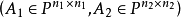
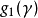
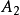
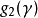
⑦r級Jordan塊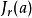的最小多項式就是它的特徵多項式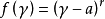，也是它的初等因子。

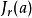
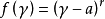
套用

最小多項式的求解方法

方法一：

（1）先將A的特徵多項式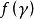在P中作標準分解，找到A的全部特徵值，，，；

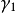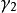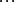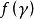
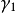
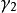
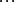
（2）對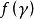的標準分解式中含有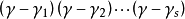的因式按次數從低到高的順序進行檢測，第一個能零化A的多項式就是最小多項式。

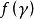
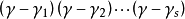
方法二：

設A是n級複數矩陣，則A的最小多項式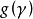是A的最後一個不變因子。

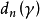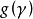
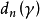
例題

求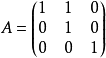的最小多項式。

解：A的特徵多項式為：

又，

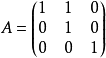
故A的最小多項式為。