基本介紹
- 中文名:自由對象
- 外文名:free object
- 學科:數學
- 性質:抽象代數的基本概念之一
- 分類:自由群、張量代數等
- 相關名詞:群
簡介
定義
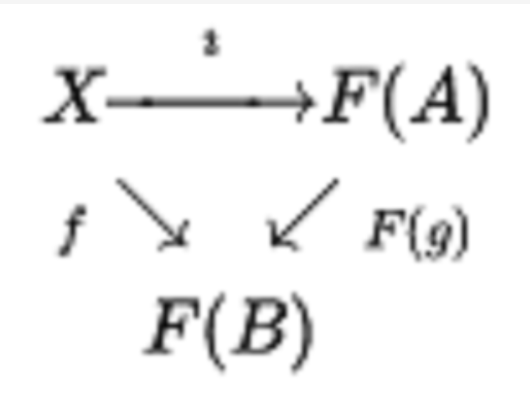
舉例









一般情況下
自由因子


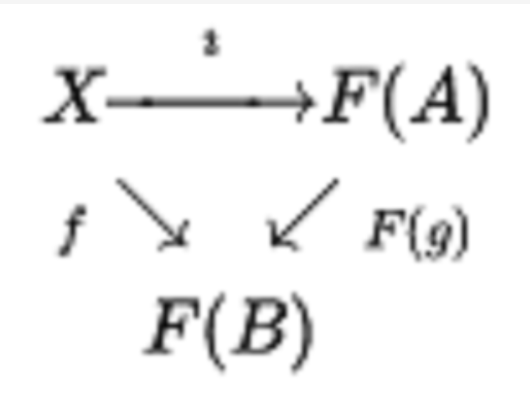











在數學中,自由對象的概念是抽象代數的基本概念之一。它是泛代數的一部分,在某種意義上它涉及到所有類型的代數結構。它在範疇論方面也有一個公式,儘管那是更為抽象...
自由戀愛是指未婚的男女雙方當事人,經別人介紹或自己遇到合適的人,從相見到相識,產生好感並發展到戀愛關係,談婚論嫁的過程中,以平等尊敬的態度對待彼此,不受他人...
自由,拼音是zì yóu,漢語詞語,英文是freedom/liberty,自由是一個政治哲學(political philosophy)概念,在這個條件下人類可以自我支配,憑藉自身意志而行動,並為對自身...
自由職業者(Self-employed)是指自己雇用自己,香港人譯作“自僱人士”。根據《韋氏大詞典》,自由職業者是腦力勞動者(作家、編輯、會計等)或服務提供者,不隸屬於...
民主對象是享有民主的主體。通常指在政治上處於統治地位的階級和階層。依法享有廣泛的政治權利和自由以及管理國家和社會經濟文化方面的權利。不同性質的國家享有民主的...
自由組合規律(law of independent assortment)是現代生物遺傳學三大基本定律之一。當具有兩對(或更多對)相對性狀的親本進行雜交,在子一代產生配子時,在等位基因分離...
自由的人性觀念三個角度:人的一般本質以整個宇宙甚至包括人本身作為參照系;人的類的本質則主要以人之外的生物作為參照系;人的社會本質則側重於單個人與社會的關係...
新自由戀愛主義事件影響 編輯 l 幫助男性破冰,走出婚戀第一步有緣網在初次溝通的男女之間巧妙搭建了最為簡潔的破冰橋樑:男性用戶只要選擇心儀的對象,就能知道對方最...
自由意是由深圳市源印科技於2012年3月份創建,致力於為國內外酒及食品的文化創意機構、個人和有需求的企業主創意交易,提供網路中介服務,成功為數萬家企業、個人提供...
自由高達是ZAFT軍在得到地球聯合軍的高達數據資料後開發的高達中的一架,其出力在突擊高達的4倍之上。機體兩肩各設一門M100型等離子光束加農炮,腰部還裝有兩門MMI...
契約自由原則(Freedom of Contract),是近代民法的一項基本原則。近代意義上的“契約自由原則”,可以追溯到1804年頒布的《法國民法典》。個人之間的契約關係,應根據...
自由質點模型質點是實際物體的“代理人” 用它代替實際物體帶有某種近似性.但是,這種近似所付出的微小代價,卻使我們獲得了巨大的收益.它使我們的研究對象變得非常...
自由遷徙已經是中國大規模城鎮化進程中的現實,農民工雖然實現了自由遷徙,但沒有享受到公平的待遇,背後是制度問題。全國農民工超過2.6億人,其中到本鄉鎮以外地方...
一般指某城市由於有關國家利害衝突,經有關國家協商宣布為獨立單位。如第一次世界大戰後的波蘭的但澤(今稱格但斯克)就曾經是自由市。自由市具有暫時的或過渡的性質...
《自由》是由阿爾伯特·塞拉執導的電影,於2019年5月18日在坎城國際電影節一種關注單元首映。...
三 資料介紹/10四 研究時段、對象及概念的界定/12五 研究理論與方法/17六 研究思路、框架與創新點/20上卷 傳統與萌動第一章 清代傳統婚姻的歷史審視/25...
自由車是指靠人力腳踏驅動,至少有兩個車輪,利用手把和前叉轉向的一種陸地交通工具。1818年德國的德賴斯發明木製、帶車把的兩輪腳踏車,依靠騎車人的雙腳蹬地行駛;...
自由旋轉是指將所選對象旋轉至任意角度。... 自由旋轉是指將所選對象旋轉至任意角度。目錄 1 自由旋轉圖形 ▪ 使用手柄 ▪ 旋轉90°方法 ▪ 自選圖形...
《向著自由》是科西嘉和巴斯克的民族解放運動中的歌曲。歌曲整體基調憂傷而又奮進,帶有濃厚的民族主義政治色彩。...
《自由的軌跡》是2011年出版的一本圖書,作者是吳小坤。... 該書選取表達自由思想的形成過程作為研究對象,借鑑發生學的方法,以傳播學的角度為切入,對英國近代表達...
動力自由度是能夠確定體系中所有運動質量相對位移所需的獨立位移的數目。... 動力自由度的研究對象是運動質量,因為慣性力的產生來源是質量;而靜力自由度的研究對象則...
自由高達是ZAFT軍在得到地球聯合軍的高達數據資料後開發的高達中的一架,其出力在突擊高達的4倍之上。機體兩肩各設一門M100型等離子光束加農炮,腰部還裝有兩門MMI...
歐洲HIP-HOP、VIDEO CLIP DANCE 錦標賽集體舞、獨舞冠軍本片由歐洲街舞錦標賽獨舞冠軍Nadin Dreimann帶您學跳最正宗、最流行的自由街舞。這些舞技招式你會經常在...
泛代數是以一般代數系統為研究對象的一個數學分支。在諸如矩陣群、置換群、變換群等具體的群概念基礎上,經過抽象概括而得出抽象群的概念,與此類似,可以在一般的群...
