基本介紹
描述
定義
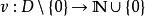

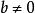



例子


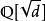
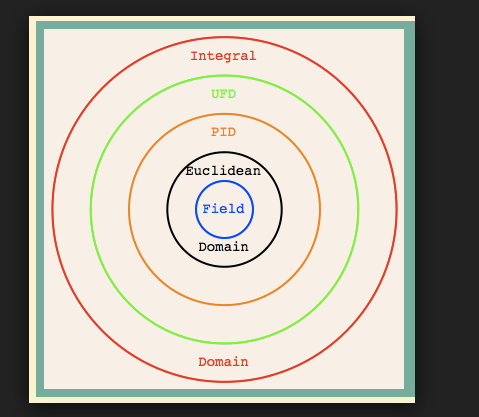
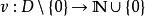

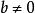





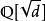
在抽象代數中,歐幾里得整環(Euclidean domain)是一種能作輾轉相除法的整環。凡歐幾里得整環必為主理想環。...
高斯證明復整數環Z[i]也有唯一分解定理。 它也誘導了諸如唯一分解整環,歐幾里得整環等等概念。 更一般的還有戴德金理想分解定理。 [3] ...
戴德金還率先定義了歐幾里得整環的概念。19世紀末,輾轉相除法的輝煌逐漸被戴德金的理想取代。輾轉相除法的其他套用發展於19世紀。1829年,施圖姆將輾轉相除法用於...
(主線為理想,講了素理想,極大理想,歐幾里得整環,主理想整環,因子分解整環等),域論(主線為域擴張,講了域擴張的途徑,域擴張的性質,域擴張的自同構群,伽羅瓦...
它也誘導了諸如唯一分解整環,歐幾里得整環等等概念,更一般的還有戴德金理想分解定理。合數合數的判定 編輯 合數可分成基本合數(能被2和3 整除的),陰性合數(加1能...
習題4-4 主理想整環與歐幾里得整環習題4-5 唯一分解整環上的多項式環第5章 域的擴張習題5-1 向量空間習題5-2 擴域習題5-3 代數擴張...
它也誘導了諸如唯一分解整環,歐幾里得整環等等概念。 更一般的還有戴德金理想分解定理。質數公式素數等差數列 等差數列是數列的一種。在等差數列中,任何相鄰兩項的...
若R是域,則 R[X] 是主理想環(事實上還是個歐幾里得整環)。 [3] 若R是唯一分解環,則 R[X] 亦然。若R是整環,則 R[X]亦然。...
韓世安, 林磊編寫的近世代數2004年出版於科學出版社.本書系統介紹了群、環、域...§4·4主理想整環與歐幾里得整環 §4·5*惟一分解整環上的多項式環 高斯小傳...
8.7 歐幾里得整環 127 8.8 域及其他的代數結構 128 8.9 本章要點 129 第9章 整理數學知識 132 9.1 證明 132 9.2 數學史上的第一個定理 135 9.3 歐幾里得...
