基本介紹
- 中文名:一一對應
- 外文名:one-to-one correspondence
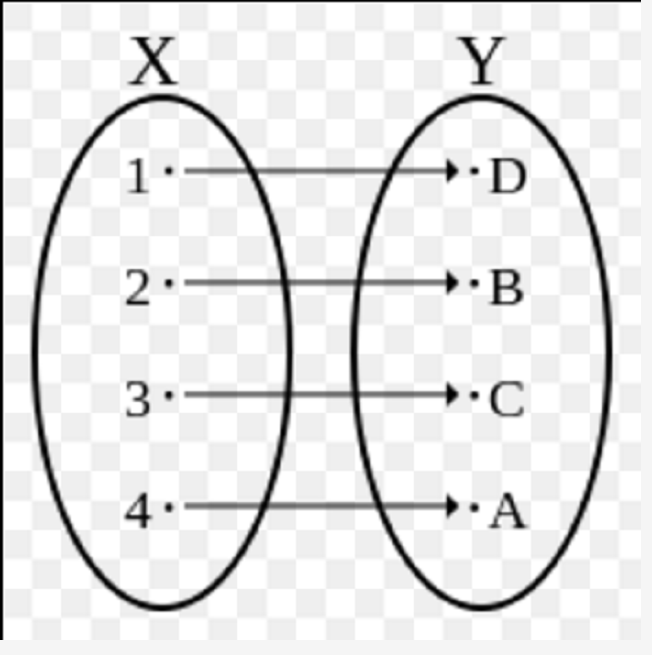
一一對應是一種常見的對應,指兩集合元素之間有一對一關係的對應。在數學中,雙射,雙射函式或一對一對應是兩組的元素之間的函式,其中一組的每個元素與另一組的...
一多對應(one-many correspondence)亦稱多值對應,是一種重要的對應,指逆對應是多一的對應,對於對應Γ=〈X,Y,G〉的值域R(Γ)中的任何元素y,集G-1(y)為...
等距對應(isometric correspondence),數學專業辭彙,是指保持長度不變的一種對應。對於兩張對應的曲面,若它們對應著的弧段總是具有相等的弧長長度,則稱這個對應是兩...
《冒險島數學奇遇記13:一一對應的全等》內容簡介:已經滅絕的恐龍竟然也出現了。哆哆和朋友們來到了一個叫桌面山的地方,遇到了“比花還要漂亮的恐龍”——“花...
單值對應又稱“映射”。對於集合A中的任何一個元素,在集合B中都有唯一的元素與它對應,這種對應關係叫做從集合A到集合B的單值對應。如,A={1,2,3},B={4,...
一維射影對應(one-dimensional projective correspondence)是透視對應的推廣,兩個一維基本形(點列或線束)間的一一對應是射影對應的充分必要條件是任何四元素的交比...
設f是從集合A到集合B的一一對應,對於B中的每一個元素b,使在A中b的原象a和它對應(f(a)=b的A的元素是唯一確定的,使這樣的b和a相對應)的對應就叫f的逆...
透視對應(perspective correspondence)是一種特殊的射影對應,設l與l′是同一平面上的兩條直線,在l與l′上各添加一個無窮遠點,就可以由中心投影建立直線l上的點...
射影對應是射影幾何中最重要的一種對應,通常指射影空間(平面、直線)之間保持共線性和共線四點的交比不變的點的一一對應。當兩個對應的射影空間(平面、直線)...
當兩個全等圖形完全重合時,相互重合的頂點叫做對應頂點,互相重合的邊叫做對應邊,互相重合的角叫做對應角。實際上,不僅全等三角形有對應邊和對應角,相似三角形中也有...
格林對應(Green correspondence)有限群與其子群之間的一類不可分解模間的對應關係.設G是一個有限群,R是一個完備局部整環(即在局部整環R模V上定義一個距離函式d...
可數集(Countable set),是指每個元素都能與自然數集N的每個元素之間能建立一一對應的集合。如果將可數集的每個元素標上與它對應的那個自然數記號,那么可數集的元素...
佛教術語,指色,聲,香,味,觸,法。與六根一一對應。“入”是吸入,有專注之義。...... 與六根一一對應。“入”是吸入,有專注之義。中文名 六入 派別 佛學 ...
