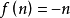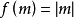單值對應

單值對應又稱“映射”。對於集合A中的任何一個元素，在集合B中都有唯一的元素與它對應，這種對應關係叫做從集合A到集合B的單值對應。如，A={1,2,3}，B={4,6,8}。A的元素按對應關係x→2x+2與B的元素對應，是單值對應。A={-1,0,1}，B={0,1,2,3}，A的元素按對應關係x→x²與B的元素對應，也是單值對應。在從A到B的單值對應下，A中的元素所對應的B中的元素b，叫做a的象，a叫做b的原象。

基本介紹

• 中文名：單值對應
• 外文名：single valued correspondence
• 所屬領域：數學（集合論）
• 別名：映射
• 相關概念：集合、映射、對應等

基本介紹

定義

設 是集合A到集合B的一個對應，對於集合A的每一個元素a，在 下都有集合B中唯一的元素b與之對應，則稱對應 是單值對應，如圖1 、 3，單值對應也叫做映射。在單值對應下，A中的元素a所對應的B中的元素b叫做a的象，a叫做b的原象。

一一對應：設A，B是兩個集合， 是從集合A到集合B的單值對應，如果對於集合A的不同元素，在B中有不同的象，而且B中的每一個元素都有原象，這個單值對應就叫做從A到B的一一對應，如圖。

逆對應：設 是從集合A到集合B的一一對應，對於B中每一個元素b，使在A中b的原象a和它對應。這樣所得顯然 也是 的逆對應。

圖1

圖2

圖3

舉例分析

下面用圖來表示從集合A到集合B的對應的幾種情況:

圖4單值對應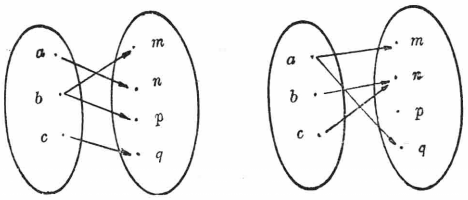

圖5

考察上述四種對應關係，我們發現前兩種對應關係和後兩種對應關係有不同的特點。圖4這兩個對應的特點是：對於集A的任一個元素，集B都有唯一的元素與它對應，這樣的對應關係叫做單值對應；圖5 所表示的對應關係中，集A 的一個元素可以與集B中的兩個元素對應，這種對應不是單值對應。

例題解析

例1 設 N={自然數}，M={負整數}。

如果對於N中的每一個自然數，使它對應M中具有相同絕對值的負整數，即給定法則

則 就是N到M的一個單值對應(映射)，可記作

例2 設 I={整數}，I₁={非負整數}。

如果對於I中的每一個整數m，使它對應I₁中的| m |，即給定法則

則 是 到 的一個單值對應(映射)，可記作。