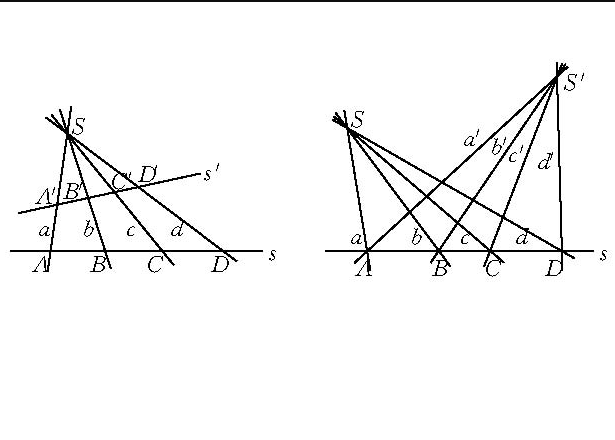
透視對應(perspective correspondence)是一種特殊的射影對應,設l與l′是同一平面上的兩條直線,在l與l′上各添加一個無窮遠點,就可以由中心投影建立直線l上的點與直線l′上的點之間的一一對應,這種通過中心投影所建立的兩直線上的點之間的一一對應稱為兩直線間的透視對應。同樣,引入無窮遠元素以後,也可以通過中心投影建立兩平面的點之間的一一對應,該對應就稱為兩平面之間的透視對應。若點列s(A,B,C,…)與線束S(a,b,c,…)在中心投影之下建立了一一對應,則稱該對應為點列s與線束S之間的透視對應,在這種透視對應中,點列s是從直線s截割線束S得到的截影,該點列稱為該線束S的透視點列,點S稱為透視中心。而線束S是從點S投影點列s而得到的投影,該線束稱為點列s的透視線束,直線s稱為透視軸,對應的點列s和線束S稱為透視的。若兩個點列s(A,B,C,…)和s′(A′,B′,C′,…)都是同一線束S的截影,則稱這兩個點列間的對應為透視對應。若兩個線束S(a,b,c,…)和S′(a′,b′,c′,…)都是同一點列s的投影,則稱這兩個線束間的對應為透視對應。
基本介紹
- 中文名:透視對應
- 外文名:perspective correspondence
- 性質:一種特殊的射影對應
- 所屬學科:數學
- 所屬問題:高等幾何(射影幾何)
定義
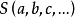
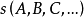
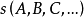
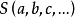
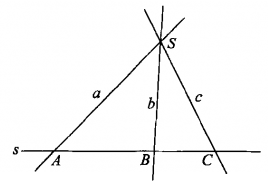 圖1
圖1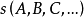
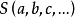
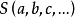
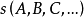
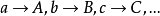
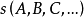
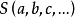
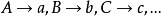
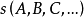
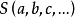
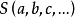
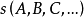
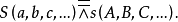
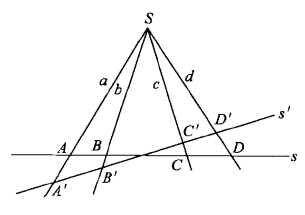 圖2
圖2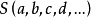

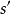
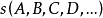
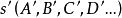
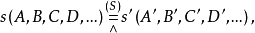
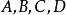
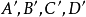
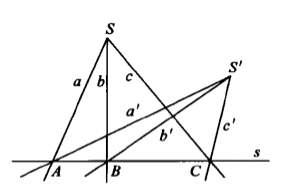 圖3
圖3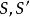
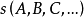
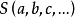
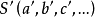
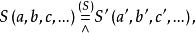
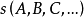
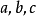
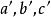
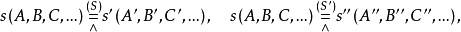
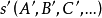
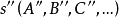
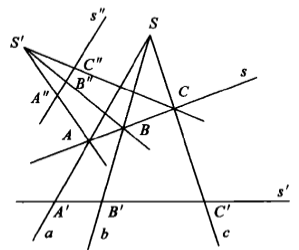 圖4
圖4