基本介紹
- 中文名:素域
- 外文名:prime field
- 所屬學科:數理科學
- 特點:不含任何真子域的域
- 別名:最小域
基本概念
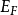
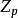
相關定理
定理1
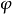
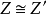
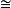
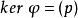
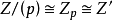
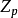
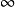
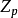
推論1
推論2
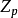
性質1
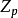
性質2
基本題型
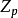
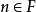

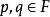
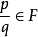
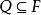
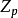
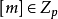
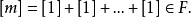
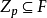
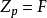
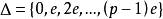
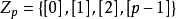
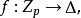
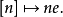

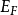
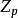
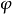
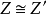
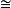
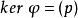
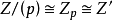
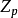
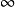
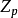
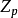
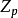
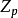
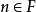

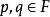
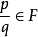
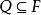
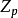
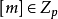
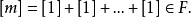
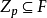
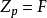
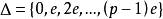
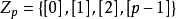
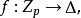
素域是一種重要的域,指不含任何真子域的域。任何一個域F都有單位元e,考慮加群{0,±e,±2e,…,±me,…},它有兩種可能:1.對任意非零整數m,me≠0,若S...
D·保素域(DarkoBozovic),黑山籍足球運動員。...... D·保素域(DarkoBozovic),黑山籍足球運動員。 中文名: D·保素域 英文名: DarkoBozovic 國籍: 黑山 ...
2006年5月,由於丹高·拉素域需要停賽,斯托伊科維奇因而在葡萄牙舉辦的2006年歐洲U-21足球錦標賽期間擔任隊長。最終球隊四強止步。國家隊斯托伊科維奇在未曾代表國家隊...
巴拉撒·保素域,男,黑山公民,出生於1987年5月1日,職位是運動員 。...... 巴拉撒·保素域,男,黑山公民,出生於1987年5月1日,職位是運動員 。中文名: 巴拉撒...
V·保素域,男,生於1981年11月13日,足球運動員,司職後衛。...... V·保素域,男,生於1981年11月13日,足球運動員,司職後衛。 中文名: V·保素域 英文...
球員:M.保素域 生日:1984年8月1日 身高:197cm 體重:91kg 加盟日期:2010-7 球衣號碼:27 國籍:黑山 效力球隊:維迪奧頓 場上位置:守門 前度效力球隊:貝爾...
基本資料球員:馬丹薜素域 生日:1980年12月27日 球衣號碼:999 國籍:波赫 效力球隊:薩連斯基 場上位置:中場球隊陣容前鋒 佩哈爾中場 蘇西奇,馬丹薜素域,阿尼西...
有限域亦稱伽羅瓦域(galois field),是僅含有限個元素的域,它是伽羅瓦(Galois,E.)於18世紀30年代研究代數方程根式求解問題時引出的.有限域的特徵數必為某一素數p...
群代數半單性定理(semisimplicity theorem ofgroup algebra)指的是群代數的雅各布森半單性判別定理。設G是群,K是域且K不是它的素域上代數,若chK=0或chK=p>0...
1 守門員 D.保素域 34 守門員 陳懷志 30 中場 亞當.雷恩布朗格 29 中場 陳樂桓 16 中場 梁敏誠 10 中場 亞哥斯達 14 中場 蔡國威 31 中場 鄭志榮 18 中...
19 中場 V.保素域 10 中場 諾瓦科維奇 18 中場 德林西奇 13 中場 米洛斯 18 中場 波積域 7 中場 西蒙·武克切維奇 2 後衛 柏維斯域 後衛 伊萬.科科傑維...
