設F是域P的非空子集,如果P的加法和乘法可看作F的加法和乖法,且對於這兩個代數運算,F也構成一個域,則稱F為P的一個子域或子體。例如,有理數域是實數域的一個子域, 而實數域又是複數域的一個子域。
基本介紹
- 中文名:子域
- 外文名:subfield
- 所屬學科:數學
- 相關概念:擴域
- 舉例:有理數域是實數域的一個子域
定義


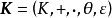





相關定理
定理1
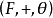





定理2





定理3

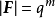





設F是域P的非空子集,如果P的加法和乘法可看作F的加法和乖法,且對於這兩個代數運算,F也構成一個域,則稱F為P的一個子域或子體。例如,有理數域是實數域的一個子域, 而實數域又是複數域的一個子域。


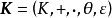





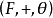















子域名(或子域;英語:Subdomain)是在域名系統等級中,屬於更高一層域的域。比如,mail.example.com和calendar.example.com是example.com的兩個子域,而example.com則...
設F是域P的非空子集,如果P的加法和乘法可看作F的加法和乖法,且對於這兩個代數運算,F也構成一個域,則稱F為P的一個子域或子體。例如,有理數域是實數域的...
城子域長城在秦皇島市北部,是四百年前戚繼光主持修建的。蒼莽的群山,溝壑縱橫雲霧繚繞,當此陣勢,果真是一夫當關萬夫莫開,。東南山腳下,是一脈蜿蜒的河流,群溪...
子域定位法用於有限元法中,是一種重要的確定加權函式的方法。 如果試探函式y(x)中含有n個待定係數,則把整個區域R分成n個子域,即 R=R1+R2+---+Rn ...
子域上阿基米德序域(Archimedean orderedfield over a subfield)是一類相對於子域具有特殊性質的序域。...
橋樑結構樣條子域法分析,責任者:丁漢山著,出版者:人民交通出版社。...... 橋樑結構樣條子域法分析,責任者:丁漢山著,出版者:人民交通出版社。橋樑結構樣條子域...
淘寶二級域名(子域名)是商家可以根據自己的需要,在不觸犯相關申請規則的情況下來設定自己的域名。有了淘寶二級域名訪問店鋪的時候,默認地址欄中就會顯示您設定的域名...
在域名前添加任何子域名,均可訪問到所指向的WEB地址。也就是客戶的域名#.com之下所設的*.#.com全部。中文名 域名泛解析 簡介 在域名前添加任何子域名 釋...
比如用戶的域名是abc.com,那么我們將主機名設定為"*",IP解析到比如:218.104.78.100,大家都知道*是通配符,他表明abc.com之前的所有子域名都將解析到218.104....
f是F的子環,且對於任意非零元素都有逆元,則f為F的一個子域,子域也是一個域。一般情況下,我們均是研究典型域下的子域。子域的判定條件:子環+任意非零元素都...
2.存在正整數m,me=0,若p是使pe=0的最小正整數,則p必為素數,稱為F的特徵(數),若S={0,e,…,(p-1)e},則S是F的子域且與整數環模p的域同構,當F=...
DMPDU尾部域由兩個子域組成,第一個是有效載荷長度子域,第二個子域是有效載荷CRC。MID用來提供從同一個IMPDU中派生出來的分割單元之間的邏輯連線,該IMPDU被傳送時...
設F是域K的子集,對於K的加法和乘法運算,F也做成一個域,則稱F是K的一個子域,K是F的一個擴域,記作K/F,稱K/F為一個域擴張。設,E/F和K/E都是域擴張...
種域(genus field)是類域的一種重要的子域。數域K的種域K定義為K的最大的如下阿貝爾擴張,它是K與一個絕對阿貝爾域K1的複合,且在K的素除子上均不分歧。...
