實數域是實數所在的有理集合,具有連續性、完備性、有序性等性質。
基本介紹
- 中文名:實數域
- 外文名:real number field
- 學科:數學
歷史,實數背景,實數的公理系統,實數域的特性,連續性,有序性,完備性,
歷史
埃及人早在公元前1000年就開始運用分數了。在公元前500年左右,以畢達哥拉斯為首的希臘數學家們就意識到了無理數存在的必要性。印度人於公元600年左右發明了負數,據說中國也曾發明負數,但稍晚於印度。在1871年,德國數學家康托爾最早地全面地給出了實數的定義。
實數背景
實數是可以用來測量連續的量的。實數的個數是無窮的。理論上,任何實數都可以用無限小數的方式表示,小數點的右邊是一個無窮的數列(可以是循環的,也可以是非循環的)。在實際運用中,實數經常被近似成一個有限小數(保留小數點後n位,n為正整數)。在計算機領域,由於計算機只能存儲有限的小數位數,實數經常用浮點數(floating point numbe)
實數的公理系統
實數可以不同方式從有理數(即分數)構作出來。設 R 是所有實數的集合,則:集合 R 是一個體:可以作加、減、乘、除、乘方運算,且有如交換律,結合律等運算律。
集合 R 是有序的:設 ,則:若
,則:若 則
則 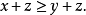


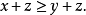
若  且
且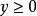 則
則 .
.

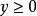

集合 R 是完整的:設 R 的一個非空的子集S,如果S在R內有上限,那么S在R內有最小上限。
最後一條是區分實數和有理數的關鍵。例如:所有平方小於2的有理數的集合存在有理數上限, 但是不存在有理數最小上限。實數是唯一適合以上特性的集合:亦即如有兩個如此集合,則兩者之間必存在代數學上所稱的域同構,即代數學上兩者可看作是相同的。
實數域的特性
連續性
數軸上的任何一點都可以用一個實數來表示,每個實數也對應著數軸上的一個點,可見全體實數正好鋪滿了數軸,這個性質稱為實數的連續性。
有序性
對於任意a,b ∈R,必滿足下述三個關係之一:
(i) a<b
(ii) a=b
(iii) a>b
對任意 ,若
,若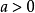 ,
, ,則存在正整數n,使得
,則存在正整數n,使得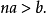

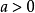

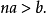
推論: 任意兩個不相等的實數間必然存在一個有理數(1)。
證明:
設 ,且
,且 。由阿基米德性,必存在自然數N,使得
。由阿基米德性,必存在自然數N,使得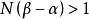 .
.


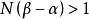
任意取定有理數 ,由於
,由於 ,a-γ(0)》0
,a-γ(0)》0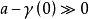 ,故存在
,故存在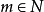 ,使得
,使得 .可見,數列
.可見,數列 中總有一項大於a.
中總有一項大於a.


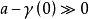
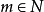


設  為此數列第一個大於α的項,於是
為此數列第一個大於α的項,於是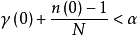 ,故
,故

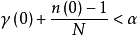

即 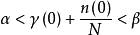 ,而
,而 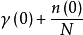 顯然為有理數,即證。
顯然為有理數,即證。
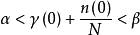
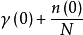
類似可以證明:任意兩個不相等的實數之間必存在一個無理數。於是有:任意兩個不相等的實數之間必有一個實數。
(1)也可以描述為:在任意一個區間(α,β)內都存在有理數。

