基本介紹
- 中文名:有限域
- 外文名:finite field
- 別稱:伽羅瓦域(galois field)
- 發現者:伽羅瓦(Galois,E.)
- 定義:僅含有限個元素的域。
- 套用領域:近代編碼、計算機理論等
概念


有限域中的計算


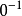
有限域的結構
相關定理
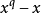
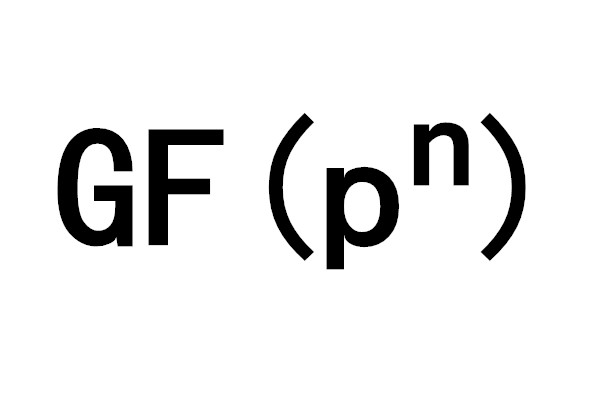




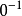
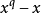
有限域亦稱伽羅瓦域(galois field),是僅含有限個元素的域,它是伽羅瓦(Galois,E.)於18世紀30年代研究代數方程根式求解問題時引出的.有限域的特徵數必為某一素數p...
本書分理論部分、套用部分兩部分,主要內容包括:來自初等數論的有限域;一般有限域;有限域上的函式;有限域上的幾何等。...
《數論、群論、有限域》是2013年清華大學出版社出版的圖書,作者是周煒。...... 同餘式,二次剩餘,原根和離散對數,群論,環、域與多項式,有限域,有限域上的線性遞...
《數論與有限域》是2010年機械工業出版社出版的圖書,作者是董麗華。...... 《數論與有限域》是初等數論與有限域的入門教材。全書共分七章,前四章論述了數論中的...
中國氣象中心高解析度有限域預報系統(HLAFS)、美國北美區域模式(Eta-12)、日本東亞譜模式(RSM)等均為有限域模式。此外,專用於熱帶氣旋位移和強度變化等的預報,也...
《代數學基礎與有限域》是2006年高等教育出版社出版的圖書,作者是林東岱。...... 《代數學基礎與有限域》是2006年高等教育出版社出版的圖書,作者是林東岱。...
《有限域和伽羅華環講義》是 2006-11-01世界圖書出版公司出版的圖書,作者是Zhe-Xian Wan。...
在邏輯上把“1”看作有限論域(limited universe of discourse),而不是無限的全體域(an unlimited universe)。他認為,無限域將包括邏輯上可能的所有領域。在這樣一...
基本信息為了促進國際學術交流,中國科學院數學與系統科學研究院將於2012年6月28日至6月30日在北京舉辦 “第五屆有限域及其套用國際研討會”(The 5th International...
《代數學基礎與有限域》是中國科學院研究生院教材,系統介紹了有限域的基本內容和基本知識。內容力求科學性、系統性、基礎性和前沿性的統一,使學習者不僅能獲得比較...
有限幾何(finite geometry)是指含有限個點的幾何結構,在組合設計理論中,所涉及的幾何結構是指一類特別的關聯繫統,這種系統中有兩類不定義的元素,分別稱為點和線,...
《有限域上典型群的幾何學》是2006年科學出版社出版的圖書,作者是WanZhexian。...... 《有限域上典型群的幾何學》是2006年科學出版社出版的圖書,作者是WanZhexian...
域論(Field Theory)是抽象代數的分支,是不少學科的基礎,是代數學中最基本的概念之一,且歷史悠久。研究域的性質,簡單地說,一個域是在其上有"加法"、"減法"、...
域多項式(field polynomial)一種特殊多項式.指在域擴張下,由一個元素所決定的多項式一個有限域擴張K/F,K可以看成F上的有限維向量空間.設w是它的一個基,對於x...
域判別式(field discriminant)判別域擴張可分性的一種工具.設w是有限域擴張K/F的一個基,T奮(a)表示元素aEK在F上的跡,行列式det (w)稱為基{yn}的判別式....
