基本介紹
- 中文名:拋物子群
- 外文名:Borel subgroup
- 領域:數學
- 性質:閉子群
- 條件:若且唯若陪集空間G/P是完備簇
- 相關名詞:博雷爾子群
簡介,分組拋物線,舉例,Lie代數,
簡介
拋物子群(parabolic subgroup)是代數群的一類閉子群。指代數群G的含有博雷爾子群的閉子群。若且唯若陪集空間G/P是完備簇,一個閉子群才是拋物子群。若P是簡約代數群G的拋物子群,則可找到P的一個簡約的閉子群(不是惟一確定的),使得P是1與V的半直積。P的這個分解稱為列維分解。當基域K的特徵數是時,任何連通代數群都有列維分解。
在代數組的理論中,代數組G的拋物子群是最大的Zariski閉合和連線的可解代數子群。 例如,在組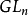 (n×n可逆矩陣)中,可逆上三角矩陣的子組是拋物子組。
(n×n可逆矩陣)中,可逆上三角矩陣的子組是拋物子組。
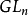
對於在代數閉合欄位上實現的組,有一個Borel子組的共軛類。
在Jacques Tits的具有(B,N)對的組的理論中,Borel子群是理解簡單(更一般地,還原)代數組的結構的兩個關鍵成分之一。 這裡B組是Borel亞組,N是包含在B中的最大圓環的歸一化。
這個概念由Armand Borel介紹,他在代數群體理論的發展中發揮了主導作用。
分組拋物線
Borel子組B和環境組G之間的子組稱為拋物線子組。在代數子群中,拋物線亞群P的特徵還在於G / P是一個完整的種類。在代數閉合的領域中,Borel子群在這個意義上證明是最小的拋物線亞群。因此,當均勻空間G / B是“儘可能大”的完整品種時,B是Borel子群。
對於簡單的代數組G,拋物線子組的共軛類的集合是與相應的Dynkin圖的所有節點子集的雙射;Borel子組對應於空集合,G對應於所有節點的集合。 (通常,Dynkin圖的每個節點確定簡單的負根,因此確定G的一維“根組”,因此節點的子集因此產生由B生成的拋物線子組和相應的負根組。此外,任何拋物線亞組與這樣的拋物線亞組共軛。)
舉例
讓 。G上的Borel子組B是上三角矩陣的集合:
。G上的Borel子組B是上三角矩陣的集合:


並且包含B的G的最大正確拋物線子群是:



此外,B中的最大環面是:

應該很清楚,這與代數圓環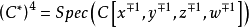 是同構的。
是同構的。
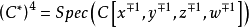
Lie代數
給出了一個具有卡丹代數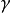 的Lie代數g的特殊情況。給定
的Lie代數g的特殊情況。給定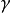 的排序,Borel子代數是
的排序,Borel子代數是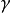 的直接總和,且g的權重空間為正。 包含Borel子代數的g的一個Lie代數被稱為拋物線代數。
的直接總和,且g的權重空間為正。 包含Borel子代數的g的一個Lie代數被稱為拋物線代數。