簇代數

在20世紀初，Fomin和Zelevinsky發明了一類新的代數，稱為簇代數。其動機是代數群中的總正性和量子群中的正則基。簇代數自問世以來，已在泊松幾何、泰克勒理論、熱帶幾何、代數組合學、顫振表示理論和有限維代數等多種場合得到了廣泛的套用。

基本介紹

• 中文名：簇代數
• 外文名：Cluster Algebra

簇代數是構造定義的交換環，其中有一組顯著的生成器（簇變數 cluster variables）。這些生成器被分為相同有限基數的重疊子集（簇）（所討論的代數的等級 rank） ）。在這些代數中，人們發現許多代數變數的坐標環在代表理論，不變數理論，總積極性研究等方面發揮著重要作用。

箭圖（quiver）

箭圖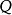 =( 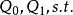)是由

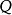
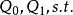
1. Q₀：一系列點或者頂點（vertices）組成
2. Q1：一系列箭頭

在這裡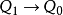， 表示每一個箭頭指向一個頂點。我們認為每一個箭圖中，不能有環（loop）或者是由兩個箭圖組成的環（2-cycle）。

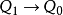
對於每個箭圖中的一個代數種，我們可以通過以下方式進行變種操作。

1. 對於每一個，加一個新的箭頭在之間。
2. 倒置每一個指向k的箭頭的方向。
3. 把新的箭圖中的 2- cycle 移除。

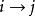
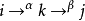
對於每一個箭圖Q，我們可以得出對於一個代數種變種兩次的箭圖，等於箭圖本身。

簇變數（cluster variables）

記（x,Q）為箭圖上的一個代數種（seed），簇變數就是 X 為箭圖里可通過變種操作的所有代數種。