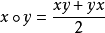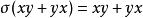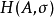定義介紹
若爾當代數(Jordan algebra)是一種交換的非結合代數。它滿足若爾當恆等式。所謂非結合代數滿足若爾當恆等式,是指對它的任意元素x,y,恆有
及
。任何交換(結合)代數都是若爾當代數。特徵數為0的域F上的任意有限維半單的若爾當代數恆可惟一地表為其單理想之直和。對於有限維若爾當代數,理想是可解的、冪零的和詣零的三條件等價。若爾當代數是20世紀30年代初由物理學家若爾當((Jordan,P.)引出來的,最初的目的是推廣量子力學的公式。
 若爾當
若爾當特殊情況
給定一個關聯代數A,可以使用相同的底層加法向量空間來構造若爾當代數
。請注意,若且唯若是交換代數時,關聯代數才是若爾當代數。如果不可交換,我們可以在A上定義一個新的乘法,使其交換,實際上使它成為Jordan代數。新的乘法x∘y滿足:
這定義了一個約旦代數
,我們稱這些為若爾當代數,以及這些若爾當代數的任何次級代數,特殊若爾當代數。所有其他約旦代數被稱為特殊的若爾當代數。 Shirshov-Cohn定理指出,任何具有兩個發生器的若爾當代數是特殊的。與此相關,麥克唐納定理指出,在每個特殊的若爾當代數中,三個變數中具有一個變數中的一個並且消失的三個變數中的任何多項式都消失。
Hermitian 若爾當代數
如果(A,σ)是具有回歸σ的關聯代數,則如果σ(x)= x和σ(y)= y,則遵循
因此,通過歸一化(有時稱為隱性元素)固定的所有元素的集合形成
的子代數,其有時表示為
。
示例
1.一組自相關實數,複數或四元數矩陣滿足如下乘法:
2.一組3×3自相關矩陣在八次數上,同樣滿足乘法
是一個二維的,特殊的若爾當代數。 這是阿爾伯特代數的第一個例子。
衍生結構代數
約旦代數A的衍生形式是A的同態D,使得D(xy)= D(x)y + xD(y)。導數形成李代數der(A)。約旦身份意味著如果x和y是A的元素,那么將z代入到x(yz)-y(xz)的同態是推導。因此,A和der(A)的直接和可以形成一個稱為A,str(A)的結構代數的李代數。
一個簡單的例子由Hermitian Jordan代數H(A,σ)提供。在這種情況下,具有σ(x)= - x的A的任何元素x定義了導數。在許多重要的例子中,H(A,σ)的結構代數為A。
正式情況
如果滿足一個n個正方形的總和只有在每個單獨消失的情況下才能消失,那么實數上的(可能非關聯的)代數就被認為是正式的。在1932年,若爾當試圖用量化理論來公理化,說任何量子系統的可觀測量的代數都應該是一個正式的實數代數,它是可交換的(xy = yx)和冪關聯(關聯法僅適用於涉及x的產品任何元素x的權力被明確定義)。他證明任何這樣的代數是若爾當代數。
並不是每個若爾當代數都是正式的,而是若爾當,馮·諾依曼和維格納(馮·諾依曼和維格納)(1934)將有限維正式的若爾當代數歸類。每個正式的真正的若爾當代數都可以寫成所謂的簡單代數的直接總和,它們本身並不是直接的,並不是平凡的。在有限的維度上,簡單的正式的若爾當代數來自四個無限的組合,連同一個例外情況:
n×n自相關實數矩陣的若爾當代數如上。
n×n自相關複數矩陣的若爾當代數如上。
n×n自相關四元數矩陣的若爾當代數。如上。
約旦代數由Rn與關係自由產生
其中右側使用Rn上的通常的內積來定義。這有時被稱為自旋因子或Clifford類型的若爾當代數。
如上所述的3×3自相關八次矩陣的若爾當代數(一個特殊的若爾當代數叫做阿爾伯特代數)。
在這些可能性中,到目前為止,似乎自然僅僅使用n×n個複雜矩陣作為可觀察的代數。然而,自旋因子在狹義相對性中起作用,所有正式的實際若爾當代數與投影幾何有關。
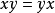
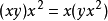
 若爾當
若爾當