置換矩陣

在數學上，特別是在矩陣理論中，置換矩陣是一個方形二進制矩陣，它在每行和每列中只有一個1，而在其他地方則為0。

設P 是一個 m×n 的 (0,1) 矩陣，如果 m≤n且 PP′=E，則稱 P為一個 m×n的置換矩陣。其中P′是P的轉置矩陣，E是m階單位方陣。

基本介紹

• 中文名：置換矩陣
• 外文名：permutation matrix
• 條件：m×n 的矩陣如 m≤n且 PP′=E
• P′是：P的轉置矩陣
• E是：m階單位方陣
• 類別：數學術語

判定定理

定理 1 當 m≦n時，一個 m×n 的(0,1) 矩陣P為置換矩陣的充要條件是P的每一行恰有一個 1，每一列恰有一個 1。

置換矩陣在數學中的矩陣論里，置換矩陣是一種係數只由0和1組成的方塊矩陣。置換矩陣的每一行和每一列都恰好有一個1，其餘的係數都是0。在線性代數中，每個n階的置換矩陣都代表了一個對n個元素（n維空間的基）的置換。當一個矩陣乘上一個置換矩陣時，所得到的是原來矩陣的橫行（置換矩陣在左）或縱列（置換矩陣在右）經過置換後得到的矩陣。

嚴格定義

每個n元置換都對應著唯一的一個置換矩陣。設π 為一個n元置換：

給出其映射圖：

它對應的n × n的置換矩陣Pπ是：在第i橫行只有π(i)位置上係數為1，其餘為0。即可以寫做：

其中每個表示正則基中的第j個，也就是一個左起第j個元素為1，其餘都是0的n元橫排數組。

由於單位矩陣是

置換矩陣也可以定義為單位矩陣的某些行和列交換後得到的矩陣。

性質

對兩個n元置換π 和 σ的置換矩陣Pπ 和Pσ，有

一個置換矩陣Pπ 必然是正交矩陣（即滿足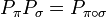

），

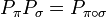
並且它的逆也是置換矩陣：

用置換矩陣Pπ右乘一個列向量 g所得到的是 g 的係數經過置換後的向量：

用置換矩陣Pπ左乘一個行向量 h 所得到的是 h 的係數經過置換後的向量：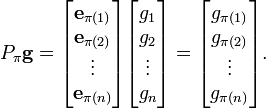

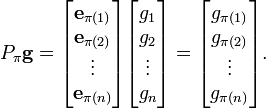
置換矩陣與置換

設Sn是n次對稱群，由於n置換一共有n! 個，n階的置換矩陣也有n! 個。這n! 個置換矩陣構成一個關於矩陣乘法的群。這個群的單位元就是單位矩陣。設A是所有n階的置換矩陣的集合。映射Sn → A ? GL(n, Z2)是一個群的忠實表示。

對一個置換σ，其對應的置換矩陣Pσ是將單位矩陣的橫行進行 σ 置換，或者將單位矩陣的橫行進行 σ 置換得到的矩陣。

置換矩陣是雙隨機矩陣的一種。伯克霍夫-馮·諾伊曼定理說明每個雙隨機矩陣都是同階的置換矩陣的凸組合，並且所有的置換矩陣構成了雙隨機矩陣集合的所有端點。

置換矩陣Pσ的跡數等於相應置換σ的不動點的個數。設 a1、a2、……、ak 為其不動點的序號，則ea1、ea2、……、eak 是Pσ的特徵向量。

由群論可以知道，每個置換都可以寫成若干個對換的複合。由此可知，置換矩陣Pσ都可以寫成若干個表示兩行交換的初等矩陣的乘積。Pσ的行列式就等於 σ 的符號差。

例子

對應於置換π = (1 4 2 5 3)的置換矩陣Pπ 是

給定一個向量 g，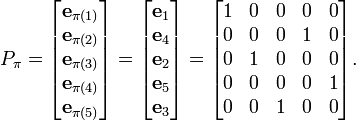

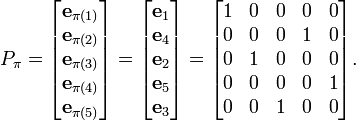
推廣

置換矩陣概念的一個推廣是將方陣的情況推廣到一般矩陣的情況：

一個m×n的0-1矩陣 P 是置換矩陣若且唯若 這時一個0-1矩陣是置換矩陣若且唯若它的每一行恰有一個1，每一列至多有一個1。

置換矩陣概念的另一個推廣是將每行的1變為一個非零的實數：

一個n階的方塊矩陣 P 是置換矩陣若且唯若其每一行與每一列都恰好只有一個係數不為零。 這時的置換矩陣P可以看做由0和1組成的置換矩陣Q與一個對角矩陣相乘的結果。