函式行列式是n元函式對每個自變數求偏導數構成的n維矩陣的行列式,也被稱為雅克比行列式。它是坐標變換理論下的基礎內容之一,不僅在數學分析隱函式理論中發揮著重要的作用,在高等代數行列式研究中也發揮著重要的作用。
基本介紹
- 中文名:函式行列式
- 外文名:functional determinant
- 學科:數學
- 領域範圍:數學分析
- 屬性:隱函式
定義和例子
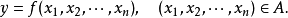
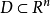
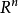


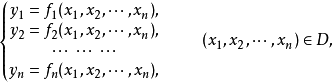
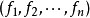
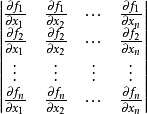
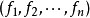
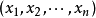
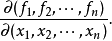
極坐標變換
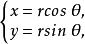
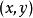
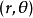

柱面坐標變換
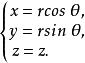
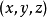
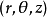
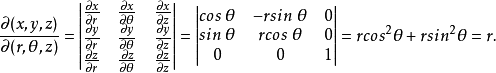
球面坐標變換
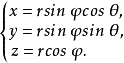
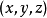

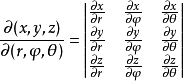
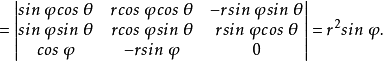
函式行列式的性質
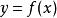
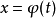

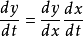
定理1
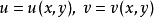
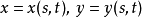
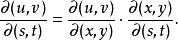
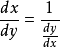
定理2
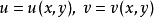
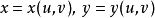
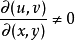
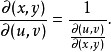
函式行列式是n元函式對每個自變數求偏導數構成的n維矩陣的行列式,也被稱為雅克比行列式。它是坐標變換理論下的基礎內容之一,不僅在數學分析隱函式理論中發揮著重要的作用,在高等代數行列式研究中也發揮著重要的作用。
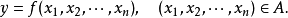
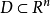
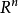


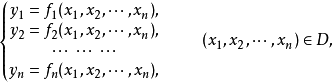
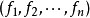
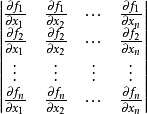
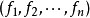
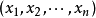
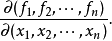
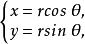
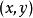
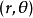

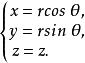
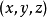
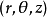
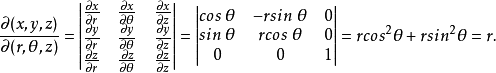
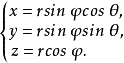
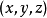

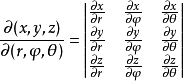
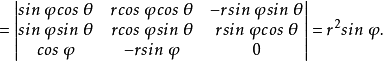
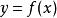
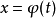

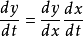
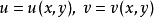
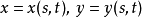
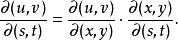
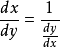
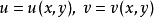
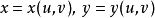
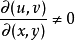
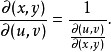
函式行列式是n元函式對每個自變數求偏導數構成的n維矩陣的行列式,也被稱為雅克比行列式。它是坐標變換理論下的基礎內容之一,不僅在數學分析隱函式理論中發揮著重要的...
行列式函式是一種特殊的多重線性函式,用行列式函式可建立與經典行列式理論等價的理論,且可使許多經典的行列式定理得到簡單的證明,使外代數在行列式理論中得到了優美的...
行列式在數學中,是一個函式,其定義域為det的矩陣A,取值為一個標量,寫作det(A)或 | A | 。無論是線上性代數、多項式理論,還是在微積分學中(比如說換元積分...
雅可比行列式通常稱為雅可比式(Jacobian),它是以n個n元函式的偏導數為元素的行列式 。事實上,在函式都連續可微(即偏導數都連續)的前提之下,它就是函式組的微分...
斯萊特行列式是多電子體系波函式的一種表達方式,他以量子物理學家斯萊特的名字命名。這種形式的波函式可以滿足對多電子波函式的反對稱要求(即所謂泡利原理):交換...
線性變換行列式是一種特殊行列式,指線性變換矩陣的行列式。設σ是數域P上的n維線性空間V的線性變換,因為相似矩陣有相等的行列式,所以可以把σ關於V的任意基的矩陣的...
弗雷德霍姆行列式(Fredholm determinant)是一個由弗雷德霍姆線性積分運算元的核確定的行列式。...
行列式在數學中,是由解線性方程組產生的一種算式。行列式的特性可以被概括為一個多次交替線性形式,這個本質使得行列式在歐幾里德空間中可以成為描述“體積”的函式。...
行列式計算器V2.0,是一款軟體,適用平台Win9x/NT/2000/XP/2003,軟體大小為69KB。...... 階以上的行列式基本不可能,而且占用資源多,運算時間與行列式的階成指數函式...
rank是T_sql 函式,rank()函式返回結果集分區內指定欄位的值的排名,指定欄位的值的排名是相關行之前的排名加一。...
在數學中,克羅內克函式(又稱克羅內克δ函式、克羅內克δ)是一個內鏈二元函式,得名於德國數學家利奧波德·克羅內克。克羅內克函式的自變數(輸入值)一般是兩個整數,...
函式的相關性(dependence of functions)幾個函式之間的相依關係,函式組(作為向量空間內的向量組)的線性相關概念的推廣。...
Excel是辦公室自動化中非常重要的一款軟體,Excel函式則是Excel中的內置函式。Excel函式共包含11類,分別是資料庫函式、日期與時間函式、工程函式、財務函式、信息函式...
det是一個計算機函式,在FreeMat、Matlab中,該函式用於求一個方陣(square matrix)的行列式(Determinant)。...
如果沒有橢圓函式理論中的一些特例為複變函數理論提供那么多的線索,那么複變函數理論的發展就會慢得多。雅可比在函式行列式方面有一篇著名的論文:《論行列式的形成與...
在向量微積分中,雅可比矩陣是一階偏導數以一定方式排列成的矩陣,其行列式稱為雅可比行列式。雅可比矩陣的重要性在於它體現了一個可微方程與給出點的最優線性逼近。...
關於線性發展的歷史,計算單元為向量(組),矩陣,行列式。...... 引進了函式行列式,即“雅可比行列式”,指出函式行列式在多重積分的變數替換中的作用,給出了函式行列式...
[2] KP方程sech函式亮孤立子 Kadomtsev-Petviashvili 方程函式解 編輯 通過朗斯基行列式展開法可得卡東塞穆夫-彼得韋亞斯維利方程多個雅可比橢圓函式解 [3] KP...
