線性變換行列式是一種特殊行列式,指線性變換矩陣的行列式。
設σ是數域P上的n維線性空間V的線性變換,因為相似矩陣有相等的行列式,所以可以把σ關於V的任意基的矩陣的行列式,稱為線性變換σ的行列式。
基本介紹
- 中文名:線性變換行列式
- 外文名:determinant of a linear transformation
- 適用範圍:數理科學
簡介
線性變換矩陣
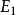




線性變換行列式是一種特殊行列式,指線性變換矩陣的行列式。
設σ是數域P上的n維線性空間V的線性變換,因為相似矩陣有相等的行列式,所以可以把σ關於V的任意基的矩陣的行列式,稱為線性變換σ的行列式。
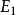




線性變換行列式是一種特殊行列式,指線性變換矩陣的行列式。設σ是數域P上的n維線性空間V的線性變換,因為相似矩陣有相等的行列式,所以可以把σ關於V的任意基的矩陣的...
行列式在數學中,是一個函式,其定義域為det的矩陣A,取值為一個標量,寫作det(A)或 | A | 。無論是在線性代數、多項式理論,還是在微積分學中(比如說換元積分...
行列式在數學中,是由解線性方程組產生的一種算式。行列式的特性可以被概括為一個多次交替線性形式,這個本質使得行列式在歐幾里德空間中可以成為描述“體積”的函式。...
變換公式(1)或(2)右邊是齊次的,在代數上叫做齊次線性變換。因此,以坐標原點作為中心的中心仿射變換的公式是行列式不等於零的齊次線性變換。反之,行列式不等於零的...
線性代數是數學的一個分支,它的研究對象是向量,向量空間(或稱線性空間),線性變換和有限維的線性方程組。向量空間是現代數學的一個重要課題;因而,線性代數被廣泛地...
《線性代數選講》將線性代數的主要內容按問題分類,通過對其若干專題的引申、強化...3.1 分塊矩陣的初等變換3.2 在逆矩陣中的套用3.3 在行列式中的套用...
本書是作者在中國科學技術大學數學系多年教學的基礎上編寫成的.它由多項式、行列式、矩陣、線性空間、線性變換、Jordan標準形、Euclid空間、酉空間和雙線性函式等九章...
非奇異線性變換(nonsingular linear transfor-mation)是一類重要的線性變換。設V是域P上的線性空間,σ∈HomP(V,V),若存在λ∈HomP(V,V),使λσ=E(單位...
1.6 利用行列式性質計算幾類行列式1.7 如何利用范德蒙行列式計算行列式...6.5 契約變換與契約矩陣6.6 正定二次型與正定矩陣第7章 線性空間和線性變換...
《線性代數》包括行列式、矩陣、線性方程組、向量空間與線性變換、特徵值和特徵向量、矩陣的對角化,二次型及套用問題等內容。...
本書內容包括行列式、矩陣和向量、線性方程組、矩陣的特徵值和特徵向量以及矩陣的對角化、實二次型、線性空間與線性變換、內積空間. 本書作為大學數學的教材和參考...
關於線性發展的歷史,計算單元為向量(組),矩陣,行列式。...... (組),矩陣,行列式,研究它們的性質和相關定理,能夠求解線性方程組,實現行列式與矩陣計算和線性變換,構...
《線性代數題型全攻略》與同濟版《線性代數》同步,包括行列式、矩陣及其運算、矩陣的初等變換與線性方程組、向量組的線性相關性、相似矩陣及二次型、線性空間與線性...
《線性代數2》是普通高等學校工科本科各專業基礎課線性代數教材,內容包括:線性空間、線性變換與矩陣、行列式及其套用、線性方程組、特徵值和特徵向量、二次型.《線性...
線性代數與解析幾何是大學數學教程系列教材的第二冊(線性代數與空間解析幾何),內容包括矩陣與行列式、向量與向量空間、線性方程組、特徵值與矩陣對角化、二次型與二...
可作為普通高等學校工科、管理、財經及非數學類理科專業的教材,也可供工程技術人員或科技人員學習參考。內容主要包括行列式、矩陣、線性方程組與向量組的線性相關性、...
一個矩陣非奇異若且唯若它的行列式不為零。一個矩陣非奇異若且唯若它代表的線性變換是個自同構。一個矩陣半正定若且唯若它的每個特徵值大於或等於零。一個矩陣...
