在數學中,克羅內克函式(又稱克羅內克δ函式、克羅內克δ)是一個內鏈二元函式,得名於德國數學家利奧波德·克羅內克。克羅內克函式的自變數(輸入值)一般是兩個整數,如果兩者相等,則其輸出值為1,否則為0。
基本介紹
- 中文名:克羅內克函式
- 外文名:Kronecker delta
- 領域:數學
簡介
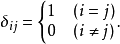
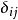
其它記法
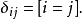
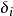
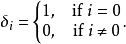
數位訊號處理
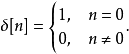
性質
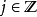
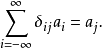

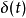
線性代數中的套用
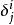
廣義克羅內克函式

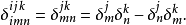
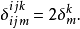
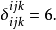

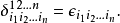
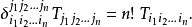
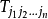

積分表示

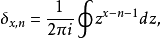
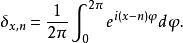
參見
- 狄拉克測度
在數學中,克羅內克函式(又稱克羅內克δ函式、克羅內克δ)是一個內鏈二元函式,得名於德國數學家利奧波德·克羅內克。克羅內克函式的自變數(輸入值)一般是兩個整數,如果兩者相等,則其輸出值為1,否則為0。
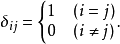
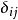
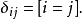
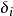
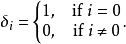
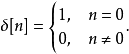
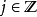
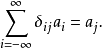

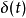
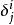

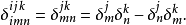
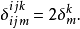
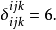

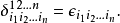
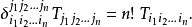
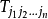


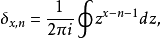
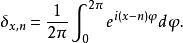
在數學中,克羅內克函式(又稱克羅內克δ函式、克羅內克δ)是一個內鏈二元函式,得名於德國數學家利奧波德·克羅內克。克羅內克函式的自變數(輸入值)一般是兩個整數,...
利奧波德·克羅內克(德語:Leopold Kronecker,1823年12月7日-1891年12月29日),德國數學家與邏輯學家,出生於西里西亞利格尼茨(現屬波蘭的萊格尼察),卒於柏林。他認為...
克羅內克指數(Kronecker index)是流形研究中的一種特定的指標。流形是一類特殊的連通、豪斯多夫仿緊的拓撲空間,在此空間每一點的鄰近預先建立了坐標系,使得任何兩...
克羅內克最主要的功績在於努力統一數論、代數學和分析學的研究。他循著N.H.阿貝爾的工作研究代數方程,用橢圓模函式解出一般五次方程;發現有理數域的任一阿貝爾擴張...
在數學中,克羅內克方法(又稱克羅內克δ函式、克羅內克δ)是一個二元函式,得名於德國數學家利奧波德·克羅內克。克羅內克函式的自變數(輸入值)一般是兩個整數,如果...
柱諧函式是正交完備的。正交性是指:其中, 為克羅內克符號, 為歸一化係數。完備性是指,對於柱坐標下的任何一個拉普拉斯方程的解均可以寫成若干個柱諧函式的線性...
克羅內克反對代數數為可數的,而超越數為不可數的證明。中文名 勒貝格-康托爾函式 領域 數學 目錄 1 數論,三角級數和序數 2 集合論 ...
本書是代數函式論的經典著作。全書共分5章:第1章介紹了關於體的一般理論;第...6 克羅內克定理//1627 代函式體的參變數的個數//1698 子體//175...
1 簡介 2 代數方面 3 克羅內克δ函式 4 李代數 McKay對應簡介 編輯 McKay對應(McKay correspondence),是一種連結幾何、組合學和代數的基本關係。基本關係解釋...
(δij為克羅內克函式)相同的態矢量內積為:狄拉克符號性質 編輯 因為每個右矢是一複數希爾伯特空間中的一個矢量,而每個右矢-左矢關係是內積,而直接地可以得到如下...
在數學中,克羅內克函式(又稱克羅內克δ函式、克羅內克δ) 是一個二元函式,得名於德國數學家利奧波德·克羅內克。克羅內克函式的自變數(輸入值)一般是兩個整數,如果...
其中εabc是列維-奇維塔符號,δab是克羅內克函式,是I是2 ×2的單位矩陣。而一樣的,上面使用了愛因斯坦求和約定。泡利矩陣內積外積關係 將泡利矩陣的對易和反對...
其中, 是克羅內克函式。注意到 與 不同,夾角 是 與空間參考系S的坐標軸單位向量 之間的夾角。變換矩陣A通常不是對稱矩陣。變換矩陣A 可以視為旋轉矩陣。例如...
一個函式列{fi:i= 1, 2, 3, ... }如果滿足:其中為克羅內克函式, 那么{fi}就稱為帶權{\displaystyle w(x)}的正交函式族。...
是克羅內克函式。從上式可以看到,機率論中的埃爾米特多項式與標準常態分配正交。埃爾米特多項式完備性 在所有滿足的函式所構成的完備空間中,埃爾米特多項式序列構成一...
克羅內克函式 金融數學上的複利 狄拉克δ函式 斯科羅霍德積分 圖中最小的角度 天文測量學上的赤緯 特納函式(Turner Function) 光程差 希臘...
為克羅內克函式。注意到如上定義中,只對數量函式 有效。我們欲將對函式的拉普拉斯運算元,延拓到微分形式上;為此,我們必須回到拉普拉斯–德拉姆運算元,將在下一節定義。...
Kronecker delta,即克羅內克函式(又稱克羅內克δ函式、克羅內克δ、克羅內克符號)δij是一個二元函式,得名於德國數學家利奧波德·克羅內克。克羅內克函式的自變數(...
兩個列維-奇維塔符號的積可以用一個以廣義克羅內克函式表示的矩陣的行列式求得:列維-奇維塔符號性質 編輯 由列維-奇維塔符號給出(共變等級為n)張量在正交基礎中...
(這裡的δmn是克羅內克函式),而正交級數傅立葉級數的收斂性 編輯 至今還沒有判斷傅立葉級數的收斂性充分必要條件,但是對於實際問題中出現的函式,有很多種判別條件...
