名稱由來
衝激回響”完全由系統本身的特性所決定,與系統的激勵源無關,是用時間函式表示系統特性的一種常用方式。
在實際工程中,用一個持續時間很短,但幅度很大的電壓脈衝通過一個電阻給電容器充電,這時電路中的電流或電容器兩端的電壓變化就近似於這個系統的衝激回響。在這種情況下,電容器兩端的電壓在很短的時間內就達到了一定的數值,然後就通過電阻放電,在此過程中,電容電壓和電路中的電流都按指數規律逐漸衰減為零。
在一般情況下,當無源系統的特性可以用一個N階線性微分方程表示時,該系統的衝激回響中包含有N個指數函式。指數中自變數(時間)的係數是實數或呈共軛對的複數,一對復係數構成一個“復頻率”,相應的兩項對應於衝激回響中的一個幅度按照指數規律衰減的正弦波。微分方程解中的常數按照系統的“初始條件”確定。為了獲得在單位衝激函式激勵下的“初始條件”,可以採用“衝激平衡原則”,就是在微分方程的等號兩邊,衝激函式和它的各階導數必須相等。因此,如果在等號右邊有衝激函式的最高階導數,那么在方程左邊回響的最高階導數中也必定包含有相同係數的這個衝激函式的最高階導數,以此類推。設回響的k階導數中含有一個幅度為A的衝激函式,那么回響的K-1階導數的初始值就等於A,以此類推,就可以得到一組有N個方程組成的,含有N個待定常數的方程組。
當激勵為單位衝激函式時,電路的零狀態回響稱為單位衝激回響,簡稱
衝激回響性質
衝激回響的雙邊傅立葉變換就是頻域
傳遞函式或系統頻域回響。
形成條件
單位衝激信號:是指在t≠0的時候,信號量恆為0,在t=0的時候,信號量為無窮大,但是信號在時間上的積分為1.
很明顯,單位衝激信號,是一種理想化的模型。引入這個模型,可以使我們在分析某系問題的時候,變得相當的簡單。比如說,信號的取樣。用f(t)表示取樣信號,用u(t)表示單位衝激信號。那么對f(t)*u(t)進行積分,就得到f(t)在0點的信號,對f(t)*u(t-x)(x表示常量)積分,就得到f(t)在x點的信號。
分類
RC並聯電路的衝激回響
當把一個單位衝激電流加到初始電壓為0的電容C上時,單位衝激電流在
到
的瞬時把IC的電荷轉移到
電容上,使得電容電壓從零躍變為1/C,即電容由原來的零初始狀態轉變到非零初始狀態。
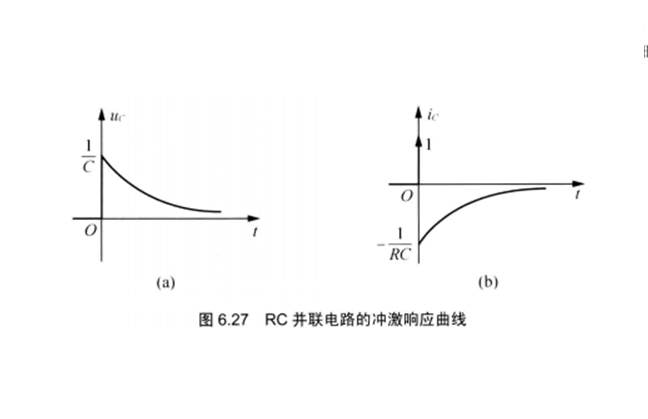 RC並聯電路的衝激回響曲線
RC並聯電路的衝激回響曲線當
後,衝擊函式為0,但是
不為零,所以電路的回響相當於換路瞬間由衝擊函式建立起來的非零初始狀態引起的零輸入回響。因此,一階電路衝激回響的求解關鍵在於計算在
衝激函式作用下的儲能元件的初始值
。
RL串聯電路的衝激回響
在衝擊電壓作用下的RL串聯電路,經分析可得電路的輸入為衝激函式時,
電容電壓和電感電流會發生
躍變。
 RL串聯電路的衝激回響曲線
RL串聯電路的衝激回響曲線不同回響關係
衝激回響與階躍回響的關係
由於
階躍函式與
衝激函式之間具有
微分和
積分的關係,可以證明,線性電路中單位階躍回響s(t)和單位衝激回響h(t)之間也具有相似的關係:
有了上述關係,就可以先求出電路的單位階躍回響,然後對時間求導,便可以得到所求得單位衝激回響。事實上,階躍函式和衝激函式之間具有的這種微分與積分的關係可以推廣到線性電路中任一
激勵與
回響中,即當已知某一激勵函式f(t)的零狀態回響r(t)時,若激勵變成f(t)的微分(或積分)函式時,其回響也將是r(t)的微分(或積分)函式。
連續時間系統
任一信號可以在時域上分解為具有不同時延的衝激信號的疊加,其衝擊強度即為衝激處的函式值
與
的乘積,從而有
實際上就是函式的卷積積分表達式,卷積的幾何解釋就是上述一系列矩形窄脈衝的求極限過程。
計算方法
電路分析法
(1)簡單電路,列出微分方程,直接求衝激回響。注意電感電流和電容電壓會產生跳變。
(2)最普遍的一種方法,利用三要素法先求出階躍回響,再對時間求導的衝激回響,即利用下式由電路的階躍回響計算出電路的衝激回響
h(t)=ds(t)/d(t)
解卷積法
卷積法是線性系統中時域分析最常用的方法之一,它可以求解系統對任意激勵信號的零狀態回響,在信號理論中占有重要地位。
設有一線性系統,其起始條件為零狀態。給該系統輸入一個單位衝激信號,可以測得輸出信號的時域信息,將單位衝激信號和輸出信號進行解卷積,就可以得到系統的單位衝激回響。


 RC並聯電路的衝激回響曲線
RC並聯電路的衝激回響曲線






 RL串聯電路的衝激回響曲線
RL串聯電路的衝激回響曲線