伴隨映射

伴隨映射(adjoint mapping)是一種映射。內積空間中的共扼映射。設E，F是域K上的內積空間，φ：E→F，φ'：F→E是線性映射。若∀ x∈E，y∈F，（φx，y）=（x，φ'y），則稱φ'稱為φ的伴隨映射。若φ'=φ，則φ稱為自伴運算元；若φ'=-φ，則φ稱為反自伴運算元。

基本介紹

• 中文名：伴隨映射
• 外文名：adjoint mapping
• 定義：內積空間中的共軛映射
• 相關：自伴運算元、反自伴運算元
• 一級學科：數學
• 二級學科：多重線性代數

內積空間

內積空間（inner product space）是歐幾里得空間的推廣。設E是域K上的向量空間，（，）是E上的雙線性函式。若（，）滿足下列條件，則E稱為內積空間，（，）稱為內積：

1、對稱性；

2、非退化性；

若E，F是域K上的內積空間，則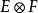 也是K上的內積空間。若 dim E=n，dim F=m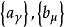， 分別是E，F的法正交基，則 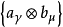是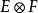 的法正交基。

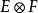
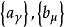
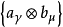
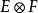
伴隨映射

伴隨映射也稱之為Hilbert伴隨映射。

設V和W是有限維度內積空間。令L∈￡(V,W)，則唯一存在一個線性映射L'：W→V使得對所有v∈V，w∈W，恆有

我們稱L'為L的Hilbert伴隨映射。

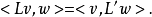
證明：對任意的w∈W，我們令映射f_w：V→F定義為

不難驗證f_w是V上的線性泛函，因此根據Riesz表現定理，存在惟一的向量x∈V使得對所有的v∈V，

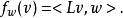
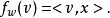
因此若我們定義映射L'：W→V為L'w=x，則對所有v∈V

這證明了L'的存在性。惟一性的證明也很容易。因為對所有的v∈V

所以 ，這表示L'線性映射，所以L'∈￡(W,V)。

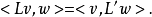
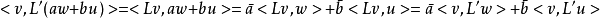
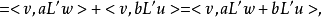
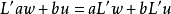
舉例

例1，令V=（Cⁿ，C），並考慮Cⁿ的標準內積。令A∈C^n×n，因為

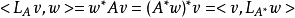
所以。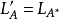

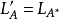
例2，令L：R^2×2→R^3×3定義為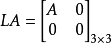，其中A∈R^2×2。

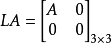
若我們定義M：R^3×3→R^2×2為MB=B₁₁，其中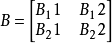而B₁₁∈R^2×2。很明顯地，L'=M。