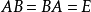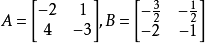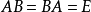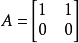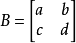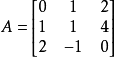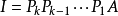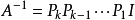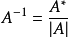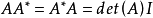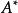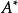定義
一個n階方陣A稱為可逆的,或非奇異的,如果存在一個n階方陣B,使得
定理
(1)驗證兩個矩陣互為逆矩陣
(2)逆矩陣的唯一性
若矩陣A是可逆的,則A的逆矩陣是唯一的。
證明:
若B,C都是A的逆矩陣,則有
(3)判定簡單的矩陣不可逆
比較其右下方一項:0≠1。
若矩陣A可逆,則 |A|≠0
若A可逆,即有A-1,使得AA-1=E,故|A|·|A-1|=|E|=1
則|A|≠0
性質
性質定理
可逆矩陣一定是方陣。
如果矩陣A是可逆的,其逆矩陣是唯一的。
A的逆矩陣的逆矩陣還是A。記作(A-1)-1=A。
可逆矩陣A的轉置矩陣AT也可逆,並且(AT)-1=(A-1)T (轉置的逆等於逆的轉置)
若矩陣A可逆,則矩陣A滿足消去律。即AB=O(或BA=O),則B=O,AB=AC(或BA=CA),則B=C。
兩個可逆矩陣的乘積依然可逆。
矩陣可逆若且唯若它是滿秩矩陣。
證明
逆矩陣是對方陣定義的,因此逆矩陣一定是方陣。
設B與C都為A的逆矩陣,則有B=C
假設B和C均是A的逆矩陣,B=BI=B(AC)=(BA)C=IC=C,因此某矩陣的任意兩個逆矩陣相等。
由逆矩陣的唯一性,A-1的逆矩陣可寫作(A-1)-1和A,因此相等。
矩陣A可逆,有AA-1=I 。(A-1) TAT=(AA-1)T=IT=I ,AT(A-1)T=(A-1A)T=IT=I
由可逆矩陣的定義可知,AT可逆,其逆矩陣為(A-1)T。而(AT)-1也是AT的逆矩陣,由逆矩陣的唯一性,因此(AT)-1=(A-1)T。
1)在AB=O兩端同時左乘A-1(BA=O同理可證),得A-1(AB)=A-1O=O
而B=IB=(AA-1)B=A-1(AB),故B=O
2)由AB=AC(BA=CA同理可證),AB-AC=A(B-C)=O,等式兩邊同左乘A-1,因A可逆AA-1=I 。
得B-C=O,即B=C。
可逆等價條件
若|A|≠0,則矩陣A可逆,且
證明:
必要性:當矩陣A可逆,則有AA-1=I 。(其中I是單位矩陣)
兩邊取行列式,det(AA-1)=det(I)=1。
由
行列式的性質:det(AA
-1)=det(A)det(A
-1)=1
則det(A)≠0,(若等於0則上式等於0)
逆矩陣求法
求逆矩陣的初等變換法
將一n階可逆矩陣A和n階單位矩陣I寫成一個nX2n的矩陣
對B施行初等行變換,即對A與I進行完全相同的若干初等行變換,目標是把A化為單位矩陣。當A化為單位矩陣I的同時,B的右一半矩陣同時化為了A的逆矩陣。
初等變換法計算原理
若n階方陣
A可逆,即A行等價I,即存在
初等矩陣P
1,P
2,...,P
k使得
比較兩式可知:對A和I施行完全相同的若干初等行變換,在這些初等行變化把A變成單位矩陣的同時,這些初等行變換也將單位矩陣化為A-1。
如果矩陣
A和
B互逆,則
AB=
BA=
I。由條件
AB=
BA以及
矩陣乘法的定義可知,矩陣
A和
B都是
方陣。再由條件
AB=
I以及定理“兩個矩陣的乘積的
行列式等於這兩個矩陣的行列式的乘積”可知,這兩個矩陣的行列式都不為0。也就是說,這兩個
矩陣的秩等於它們的級數(或稱為階,也就是說,A與B都是方陣,且rank(A) = rank(B) = n)。換句話說,這兩個矩陣可以只經由初等行變換,或者只經由初等列變換,變為單位矩陣。
伴隨矩陣法
注意:
中元素的排列特點是的第k
列元素是A的第k
行元素的
代數餘子式。要求得
即為求解
的余因子矩陣的
轉置矩陣。A的伴隨矩陣為
,其中A
ij=(-1)
i+jM
ij稱為a
ij的代數餘子式。