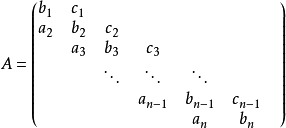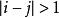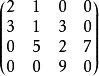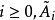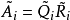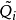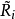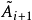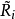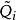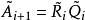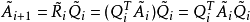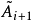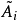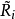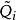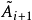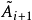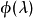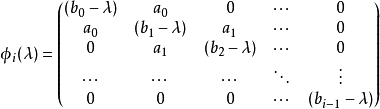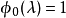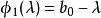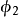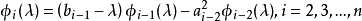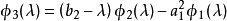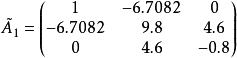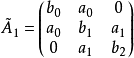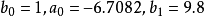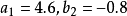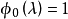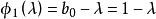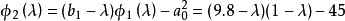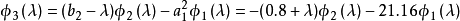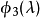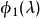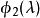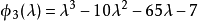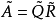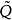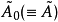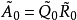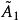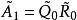三對角矩陣

在線性代數中，三對角矩陣是矩陣的一種，它“幾乎”是一個對角矩陣。準確來說：一個三對角矩陣的非零係數在如下的三條對角線上：主對角線、低對角線、高對角線。在許多物理問題中，三對角矩陣常常作為原始數據出現，因此它們本身是很重要的，這種矩陣僅有（2n-1）個獨立的元素。由三對角矩陣確定特徵值由一些較有效的方法，常見的有兩種：QR法、特徵多項式法。

基本介紹

• 中文名：三對角矩陣
• 外文名：Three diagonal matrix
• 屬性：矩陣
• 類型：數學術語
• 特點：非0元素排列在三條對角線上
• 套用領域：數值分析，工程結構動力分析

定義

形如

的n×n矩陣A稱為三對角矩陣，其中第(i,j)個元素在j>i+1和j<i-1時為零。

三對角矩陣的建立

分析矩陣特點

三對角矩陣M是一個對角矩陣，若且唯若 時，有M(i,j)=0。在一個nxn的三對角矩陣T中，非0元素排列在如下的三條對角線上：

（1）主對角線即i=j；

（2）主對角線之下的對角線（稱低對角線）即i=j+1；

（3）主對角線之上的對角線（稱高對角線）即i=j-1。

這三條對角線上的元素總數為3n-2，故可以使用一個擁有3n-2個位置的一維數組來描述T，因為僅需要存儲三條對角線上的元素。

矩陣實例

考察如下所示的4×4三對角矩陣：

三對角矩陣上共有10個元素，如果把這些元素逐行映射到t中，則有t[0:9]=[2,1,3,1,3,5,2,7,9,0]；如果逐列映射到t上，則有t[0:9]=[2,3,1,1,5,3,2,9,7,0]；如果按照對角線的次序（從最下面的對角線開始）進行映射，則有t[0:9]=[3,5,9,2,1,2,0,1,3,7]。

建立該三對角矩陣的程式

利用Store函式把傳入的x值存儲在相應的三對角矩陣中，並通過switch語句判斷其所在位置。具體程式如下：

#include "stdio.h"#define n 10int t[3*n];void Store(intx,int i,int j){//把x存為T(i,j)    if(i<1 || j<1 ||i>n ||j>n)      {printf("數組出界！");       exit(1);      }    switch(i-j){      case 1:t[i-2]=x;break;//低對角線      case 0:t[n+i-2]=x;break;//主對角線      case -1:t[2*n+i-2]=x;break;//高對角線      default:  if(x！=0)        {          printf("非對角線上元素值必須為零")；          exit(1);        }    }}void main(){  int i,j;  int D[n][n];        for(i=0;i<n;i++)              for(j=0;j<n;j++)                 Store(D[i][j],i,j);}

確定三對角矩陣的特徵值

QR法

QR法對於三對角矩陣來說是很好的，在這個方法中，矩陣被分解成以下形式： ，其中 是正交矩陣， 是上三角矩陣。產生如下的矩陣序列：將 化成乘積形式 ，則 定義為 。

一般來說，對於 化成 ，其中 是正交矩陣， 是上三角矩陣，則 被定義為 和 以相反次序乘積式，即 。因為 是正交矩陣， 。 是對稱的，與 有相同的特徵值。我們定義和成這樣的形式：是三對角矩陣，最終趨於變為對角陣，其對角線上的元素給出原矩陣的特徵值。

特徵多項式法

特徵多項式法可以像特徵多項式的根一樣確定特徵值。有一種有效的方法來構造三對角矩陣的特徵多項式。使用符號法可以求特徵值的歸類，從而形成一個Sturmian序列。然後用對分法或試位法來求精確的特徵值。由Householder變換得到的對稱三對角矩陣的特徵多項式為：

其中，i=1,2,...,n，有：

從向前的Sturm序列可以表示為：

因此，有

實例

求下述三對角矩陣的特徵多項式：

解：把該矩陣與特徵多項式的一般形式作比較，則有

比較這兩個矩陣，得到

在的表達式中代入和的值並化簡，得到：。