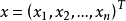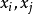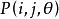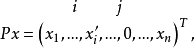基本介紹
- 中文名:吉文斯法
- 外文名:Given's method
- 所屬學科:數學
- 所屬問題:線性方程組數值解法
- 別稱:平面旋轉變換
基本介紹,吉文斯變換,
基本介紹
雅可比法是利用矩陣對角化的方法得到實對稱矩陣A的特徵值問題的解,它是基於坐標旋轉概念的一種疊代法,且當A的對角元素為主元時十分有效。吉文斯法是基於坐標旋轉概念的另一種方法,二者相比,吉文斯法實際上不能得出特徵值問題的解而只是把實對稱矩陣A簡化成三對角形式。關於三對角矩陣特徵值問題的解必須用另一種方法得到。吉文斯法的顯著優點是簡化成三對角形式時不需要進行疊代,而只需要有限的幾步運算。
雅可比方法(Jacobi's method),它系統地消除矩陣的非對角項,將對稱矩陣轉化為對角陣。遺憾的是,由於每消去一個非零元素的同時,常會將之前為零的元素變成非零的,因此該方法所需要的運算元是無窮多次。儘管經過有限次數的運算之後,矩陣的非對角元素仍不可能完全為零,但矩陣最終將收斂到對角型。因而,雅可比方法需要反覆疊代,直到非對角項“足夠”少為止。
吉文斯法(Given's method)也是一種將對稱矩陣轉化為簡單形式的方法。與雅可比方法不同的是,該方法所對應的簡單形式是三對角陣。另一個不同之處在於,吉文斯法只在殘餘的非對角位置產生零元素。因此,它所需要的運算元是有限的,從而比雅可比方法的效率更高。
豪斯霍爾德法(Householder's method)也是一種將對稱矩陣轉化為三對角形式的方法。這種方法的運算元是有限的,並且,由於它同時將整行和整列的非對角元素變成零元素,所以它比吉文斯法更為高效。
一旦用吉文斯法或豪斯霍爾德法將矩陣化為三對角系統,那么剩下的工作就是求出特徵值。比較直接的做法是,將行列式展開,從而得到一連串的多項式,通過疊代可以求出特徵值。
除了對稱矩陣之外,一般矩陣的所有特徵值也可以通過許多方法求解。它們包括:Rutishauser 的LR 方法(LR method)和Francis的QR 方法(QR method)。雖然QR方法的效率相對低一點,但由於它更加穩定,所以通常是優先使用的。如此,該方法被認為是最通用的求解方法。
最後要提到的一點是,上述方法通常是結合它們各自的特點來使用的。例如,吉文斯法和豪斯霍爾德法也可用於非對稱矩陣,不過所得結果不是三對角陣,而是一類被稱為海森伯格型(Hessenberg form)的特殊形式。另有一種方法利用了豪斯霍爾德法的速度優勢,即先用豪斯霍爾德法將矩陣轉化為三對角形式,再根據穩定的QR算法來求解特徵值。
吉文斯變換
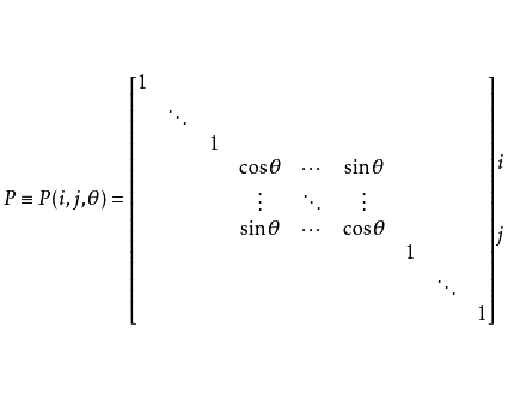
吉文斯變換(Givens transformation)亦稱平面旋轉變換,數值代數的基本工具之一,它是一種正交變換,最常用的吉文斯變換是使變換後的向量的某個分量(例如第k個)變為零。
設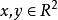 ,則變換
,則變換
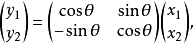

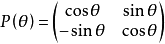
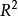
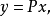
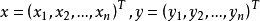
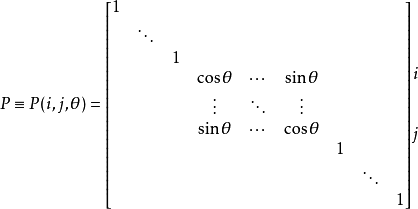
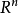
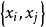
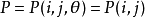
顯然,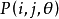 具有性質:
具有性質:
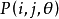
(1) P與單位陣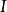 只是在
只是在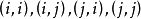 位置元素不一樣,其他相同。
位置元素不一樣,其他相同。
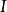
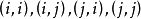
(2) P為正交矩陣 。
。

(3)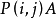 (左乘)只需計算第
(左乘)只需計算第 行與第
行與第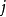 行元素,即對
行元素,即對 有
有
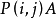
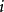
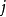

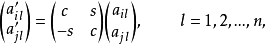
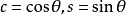
(4)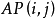 (右乘)只需計算第i列與第j列元素
(右乘)只需計算第i列與第j列元素
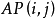
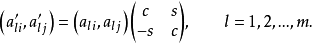

定理 (約化定理)設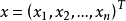 ,其中
,其中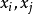 不全為零,則可選擇平面旋轉陣
不全為零,則可選擇平面旋轉陣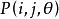 ,使
,使