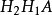豪斯霍爾德法

豪斯霍爾德法(Householder method)，是正交分解法的一種。它先線上性方程組Ax=b的兩邊施行n-1次豪斯霍爾德變換（Householder變換）將其變為等價的上三角方程組Rx=b'，然後求解Rx=b'，即可得到原方程組的解。這一方法的運算量是高斯消去法的兩倍，但其數值穩定性較好。

基本介紹

• 中文名：豪斯霍爾德法
• 外文名：Householder method
• 領域：數學
• 理論基礎：Householder變換
• 優點：數值穩定性好
• 套用：求方程組的解

Householder矩陣

一般地，在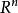 中，將向量x映射為關於“與單位向量u正交的n-1維子空間”對稱的向量y的鏡像變換定義如下：

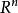
設單位向量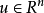 ，稱

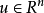
為Householder矩陣（初等反射矩陣），由Householder矩陣確定的線性變換成為Householder變換（初等反射變換、鏡像變換或反射變換）。

Householder矩陣的性質

Householder矩陣具有下列性質：

(1) （對稱矩陣）

(2)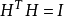 （正交矩陣）；

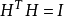
(3) （對合矩陣）；

(4)detH=-1；

(5)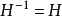 （自逆矩陣）；

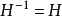
(6) 是n+r階Householder矩陣。

Householder變換舉例

已知：

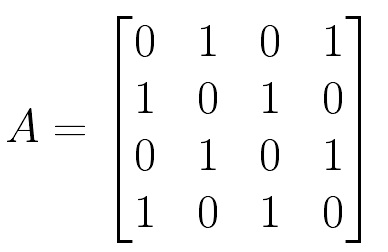
則Householder變換過程為：

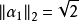1）計算H1：令，則。取λ1=，

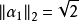
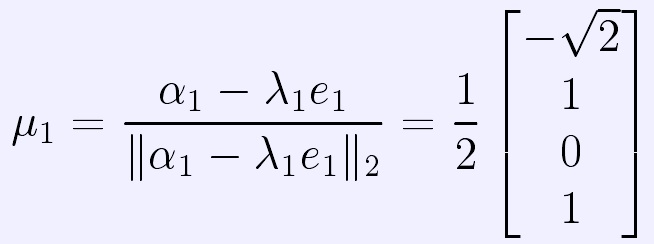
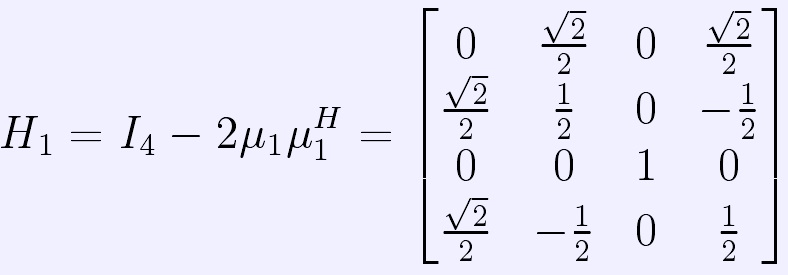
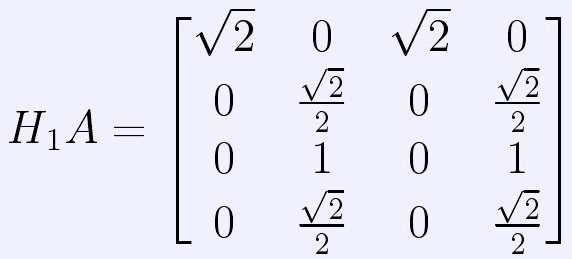
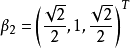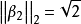2）計算H2：令，則。取λ2=，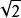

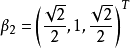
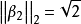
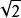
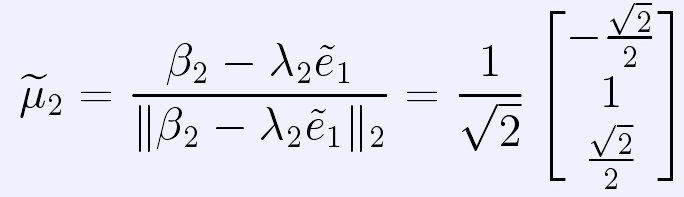
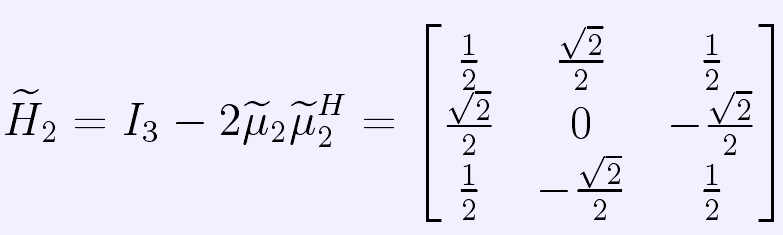
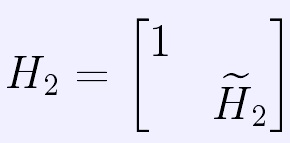
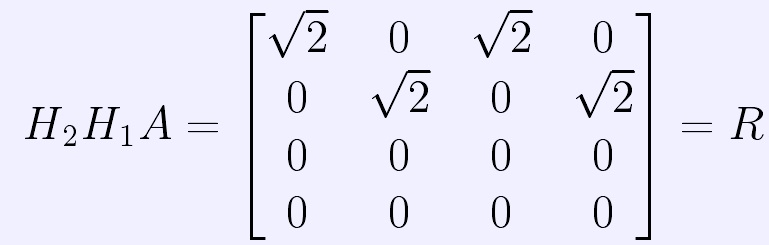
因為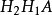是一個上三角形，所以，Householder變換到此結束。