正交分解法是:求合力的一種方法。就是將受力物體所受外力平移到平面坐標系的原點(限同一平面內的共點力)並沿選定的相互垂直的x軸和y軸方向分解,然後分別求出x軸方向、y軸方向的合力ΣFx、ΣFy,由於ΣFx、ΣFy相互垂直,可利用勾股定理方便的求出物體所受外力的合力ΣF{大小和方向}。
基本介紹
- 中文名:正交分解法
- 外文名:Orthogonal decomposition method
- 運用條件:物體受到多個方向的外力作用
- 原則:少分解力和容易分解
- 目的:用代數運算公式來解決矢量的運算
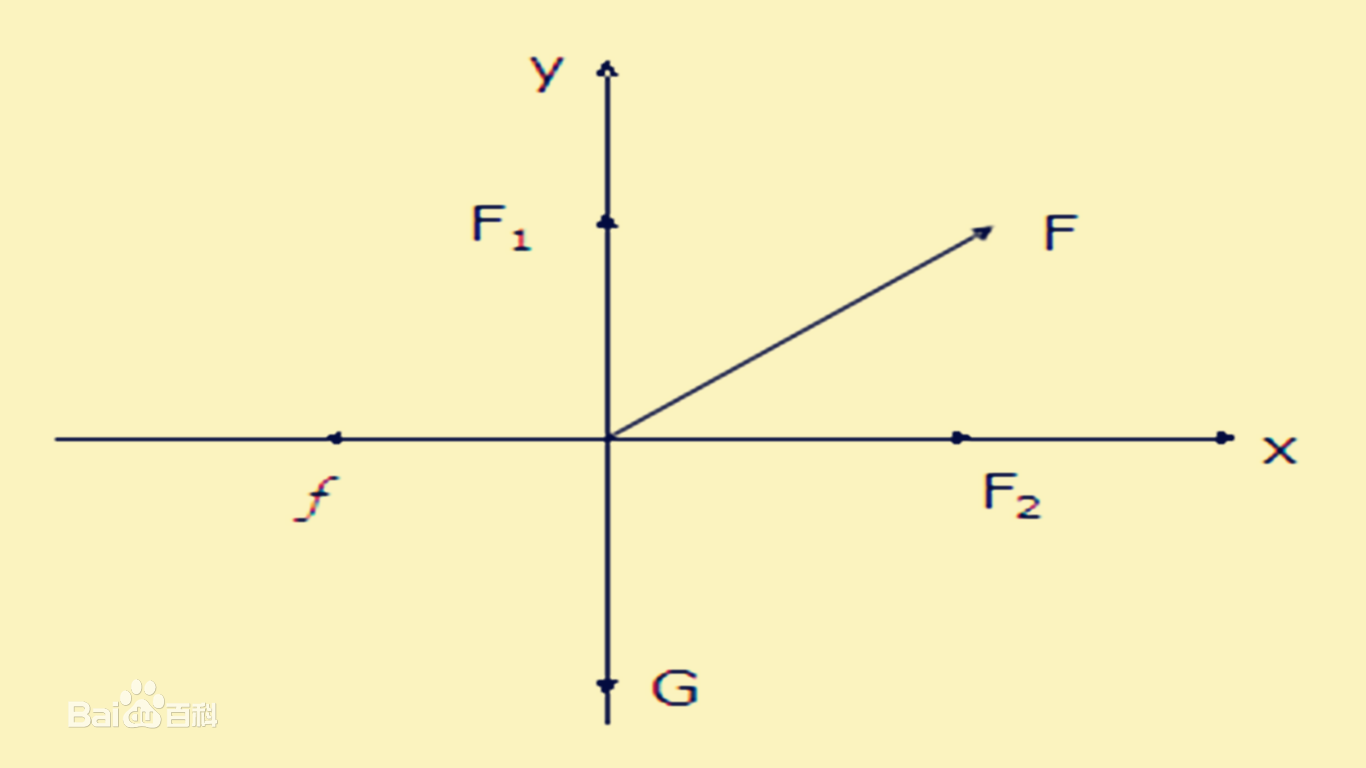
正交分解法是:求合力的一種方法。就是將受力物體所受外力平移到平面坐標系的原點(限同一平面內的共點力)並沿選定的相互垂直的x軸和y軸方向分解,然後分別求出x軸方向、y軸方向的合力ΣFx、ΣFy,由於ΣFx、ΣFy相互垂直,可利用勾股定理方便的求出物體所受外力的合力ΣF{大小和方向}。
正交分解法是:求合力的一種方法。就是將受力物體所受外力平移到平面坐標系的原點(限同一平面內的共點力)並沿選定的相互垂直的x軸和y軸方向分解,然後分別求出...
正交分解是高中物理力學的一種求解方法。全稱為“力的正交分解”。將一個力分解為Fx和Fy兩個相互垂直的分力的方法,叫作力的正交分解。從力的矢量性來看,是力F...
正交分解法 物體受到多個力作用時求其合力,可將各個力沿兩個相互垂直的方向直行正交分解,然後再分別沿這兩個方向求出合力,正交分解法是處理多個力作用問題的基本...
(注:對力按平行四邊形法則進行分解時要按力的實際效果或正交分解法進行。).合力和力的合成:一個力產生的效果如果能跟原來幾個力共同作用產生的效果相同,這個力...
除緒論外,全書共分10章,其基本內容包括輸入輸出系統理論、漸近波形估計方法、Krylov子空間類方法、多點擬合方法、正交分解方法、平衡截斷方法、積分全等變換與最最佳化...
在套用動量定理時,應該遵循矢量運算的平行四邊表法則,也可以採用正交分解法,把矢量運算轉化為標量運算。假設用Fx(或Fy)表示合外力在x(或y)軸上的分量。(或)和...
豪斯霍爾德法(Householder method),是正交分解法的一種。它先線上性方程組Ax=b的兩邊施行n-1次豪斯霍爾德變換(Householder變換)將其變為等價的上三角方程組Rx=b'...
另一類是由系統的近似樣本數據集通過構造一組基向量來對系統進行降階 , 即本徵正交分解法 (proper orthogonal decomposition, POD), 可有效地對非線性系統進行降...
吉文斯法(Givens method)是正交分解法的一種。它線上性方程組Ax=b的兩邊施行一系列吉文斯變換將其變為等價的上三角方程組,然後求解上三角方程組而得到原方程組的...
多個向量的合成用正交分解法,如果要求模一般需要先算出合成後的向量。 模是絕對值在二維和三維空間的推廣,可以認為就是向量的長度。推廣到高維空間中稱為範數。向...
常用的模型降階方法:特徵正交分解法(Proper Orthogonal Decomposition, POD)、動力模態分解法(DMD)等。其中POD方法套用最為廣泛。POD方法,也被稱為Kahunen-Loeve分解...
根據這個特點,我們求解三力平衡問題時,常用的方法是力的合成法,當然也可以用分解法(包括正交分解)、力的矢量三角形法和相似三角形法等。...
三角形等手段求解;或將某一個力分解到另外兩個力的反方向上,得到的這兩個分力勢必與另外兩個力等大、反向;對於多個力的平衡,利用先分解再合成的正交分解法。...
矢量運算,矢量之間的運算要遵循特殊的法則。矢量加法一般可用平行四邊形法則。由平行四邊形法則可推廣至三角形法則、多邊形法則或正交分解法等。矢量減法是矢量加法的...
題時,運用正交分解法較為方便。注意:發生非對心碰撞的兩個小球,可以將小球速度沿球心連線和垂直球心連線兩個方向分解,在這兩個方向上套用動量守恆定律列式求解。...
b、正交分解與牛頓第二定律c、牛頓第二定律瞬時性套用d、整體法與隔離法的套用蝸牛老師教物理視頻教程例題分析 編輯 第一章:運動的描述1-1質點、參考系典題分析...
4.共點力的平衡F合=0,推廣 {正交分解法、三力匯交原理}5.超重:FN>G,失重:FN<G {加速度方向向下,均失重,加速度方向向上,均超重}...
運用整體法解力的平衡問題 用平均速度求解運動學問題 利用v-t圖象求解運動學問題 套用正交分解法解題 全電路變化的問題 整體法解電場問題 等效法解帶電體在電場中...
還可以使用矢量三角形法,正交分解法等。利用電場的疊加原理,理論上可計算任意帶電體在任意點的場強。注意:各個電荷產生的電場是獨立的、互不影響的 對於較大的...
[3] 解題方法主要有四種:臨界條件法、正交分解法、合成法、程式法。[24] 運用牛頓第二定律及同一直線矢量合成方法,根據理想“平行導軌模型”的物理特點,基於電磁...
2.9 用對稱法求解力的平衡問題(47)2.10 力的平衡中的極值問題(50)3怎樣解運動和力問題3.1 月1正交分解法求解運動和力問題(53)...
9.2.3 奇異值分解§9.3 最小二乘問題的直接解法9.3.1 QR分解方法9.3.2 法方程法9.3.3 完全正交分解方法9.3.4 SVD方法§9.4 總體最小二乘問題的直接解法...
模板4假設法判斷摩擦力的有無及方向 模板5合力的範圍 模板6正交分解法的利用 模板7整體法和隔離法解決力的平衡問題 模板8平衡問題中的臨界和極值問題 模板...
由平行四邊形法則可推廣至三角形法則、多邊形法則或正交分解法等。矢量減法是矢量加法的逆運算,一個矢量減去另一個矢量,等於加上那個矢量的負矢量。即 A-B=A+(...
