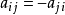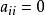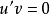基本介紹
- 中文名:反對稱矩陣
- 外文名:Skew-symmetric matrix
- 相關矩陣:對稱矩陣
- 類別:線性代數
- 特點:A(i,j)=-A(j,i)
- 套用領域:高等數學
定義,基本性質,性質1,性質2,性質3,注意事項,定理及其證明,定理1,定理2,
定義
基本性質
性質1
設A,B為反對稱矩陣,則A±B仍為反對稱矩陣。
證明過程:
設A,B為反對稱矩陣,即有


至此,根據反對稱矩陣的定義可得,A±B為反對稱矩陣。
性質2
設A為反對稱矩陣,則 仍為反對稱矩陣。
仍為反對稱矩陣。

證明過程:
設A為反對稱矩陣,即有
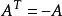
則有
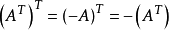

至此,根據反對稱矩陣的定義可得, 仍為反對稱矩陣。
仍為反對稱矩陣。

性質3
設A為反對稱矩陣,B為對稱矩陣,則AB-BA為對稱矩陣。
證明過程:
已知A為反對稱矩陣,B為對稱矩陣,即有

故有:

至此,根據反對稱矩陣的定義可得,AB-BA為對稱矩陣。
注意事項
(1)設A,B為反對稱矩陣,AB不一定是反對稱矩陣。
(2)設A為反對稱矩陣,若A的階數為奇數,則A的行列式為0;A的階數為偶數,則根據具體情況計算。
定理及其證明
定理1
奇數階反對稱矩陣的行列式必為0。
證明過程:
設A為反對稱矩陣,即有
設A為反對稱矩陣,即有
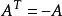
故有

當n為奇數時,就由 ,於是
,於是 。
。


定理2
證明:
(1)設實反對稱矩陣A的特徵值 ,相應的特徵值向量
,相應的特徵值向量 ,其中u,v是實向量。那么由
,其中u,v是實向量。那么由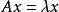 得到
得到


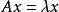

即

分別等置兩邊的實部和虛部得到

於是

因為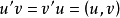 (內積),所以上二式相加得到
(內積),所以上二式相加得到
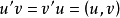
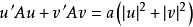
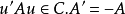



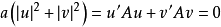
於是由 推出a=0,從而
推出a=0,從而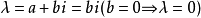 。
。

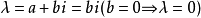
(2)由(1)中可得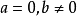 ,所以
,所以 ,即
,即
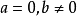


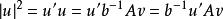

因為 ,所以
,所以 。
。