對稱矩陣的壓縮算法

矩陣是很多科學與工程計算問題中研究的數學對象，在實際套用中，經常出現一些階數很高的矩陣，同時在矩陣中有很多值相同的元素並且它們的分布有一定的規律——稱為特殊矩陣（special matrix），對稱矩陣就是其中一種。對稱矩陣的特點是：在一個n階方陣中，有aij=aji(1≤i，j≤n)。可以對這類矩陣進行壓縮存儲，從而節省存儲空間，並使矩陣的各種運算能有效進行。

基本介紹

• 中文名：對稱矩陣的壓縮算法

分析過程

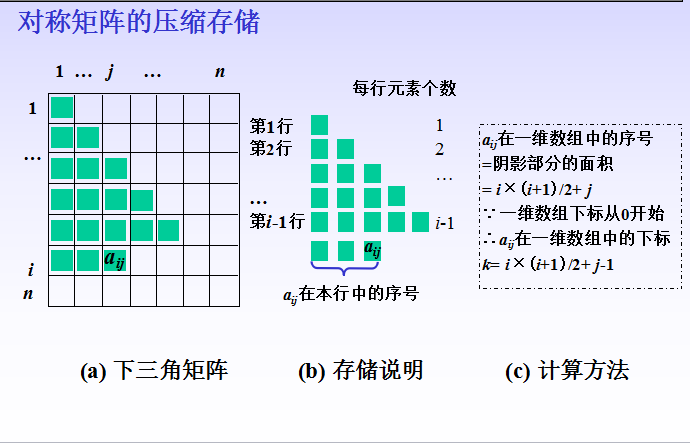
對稱矩陣關於主對角線對稱，因此只需存儲下三角部分（包括主對角線）即可。這樣，原來需要存儲n×n個存儲單元，現在只需要n×(n+1)/2個存儲單元，節約了大約一半的存儲單元。當n較大時，這是比較可觀的一部分存儲單元。

如何只存儲下三角部分的元素呢？由於下三角中共有n×(n+1)/2個元素，可將這些元素按行存儲到一個數組SA[n(n+1)/2]中。這樣，下三角中的元素aij(i≥j)存儲到SA[k]中，在數組SA中的下標k和i、j的關係為：k=i×(i-1)/2+j-1，定址的計算方法如圖所示。

算法實現

#include <iostream>

using namespace std;const int N = 5;

int main( )

{

int a[N][N], SA[N * (N + 1) / 2] = {0};int i, j;cin>>i;

for (j = 0; j < N; j++)

for (i = 0; i < N; i++)

for (j = 0; j <= i; j++)

a[i][j] = a[j][i] = i + j;

for (i = 0; i < N; i++)

{

cout<<a[i][j]<<" ";

cout<<endl;

}

for (i = 0; i < N; i++)

for (j = 0; j <= i; j++)

SA[i * (i - 1)/2 + j] = a[i][j]; //壓縮存儲

cout<<"請輸入行號和列號：";

cin>>i>>j;

cout<<i<<"行"<<j<<"列的元素值是：";

if (i >= j)

cout<<SA[i * (i - 1)/2 + j]<<endl;

else

cout<<SA[j * (j - 1)/2 + i]<<endl;

return 0;

}