方嚮導數本質上研究的是函式在某點處沿某特定方向上的變化率問題,梯度反映的是空間變數變化趨勢的最大值和方向。方嚮導數與梯度在微分學中有重要的運用。
基本介紹
- 中文名:方嚮導數與梯度
- 外文名:directional derivative and gradient
- 屬於:數學
- 運用:微積分學、幾何學等
方嚮導數
導數


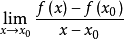
定義
















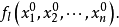
方嚮導數與偏導數、全微分的關係













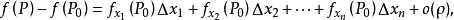


梯度
定義



梯度與方嚮導數的關係




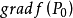




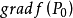




套用


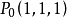


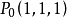



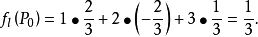




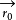


方嚮導數本質上研究的是函式在某點處沿某特定方向上的變化率問題,梯度反映的是空間變數變化趨勢的最大值和方向。方嚮導數與梯度在微分學中有重要的運用。


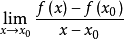
















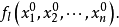













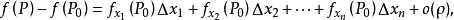









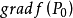




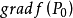






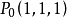


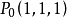



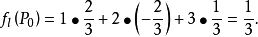






方嚮導數本質上研究的是函式在某點處沿某特定方向上的變化率問題,梯度反映的是空間變數變化趨勢的最大值和方向。方嚮導數與梯度在微分學中有重要的運用。...
2.2.1 方嚮導數 2.2.2 梯度 2.3 海森矩陣和泰勒展開式 2.3.1 海森(Hesse)矩陣 2.3.2 多元函式的泰勒展開式 習題 第3章 最優性條件 3.1 ...
在單變數的實值函式的情況,梯度只是導數,或者,對於一個線性函式,也就是線的斜率。梯度一詞有時用於斜度,也就是一個曲面沿著給定方向的傾斜程度。可以通過取向量...
5.方嚮導數與梯度 6.二元函式的Taylor公式 7.多元微分學的幾何套用 8.多元函式的極值與最值 [典型例題] [練習] [答案與提示] 第七章 重積分 [內容精講] ...
6 方嚮導數與梯度 1.方嚮導數 2.梯度 習題9.6 7 多元函式的極值與最大值及最小值 1.函式的極值 2.最大值與最小值 3.條件極值——拉格朗日乘...
9.4.4 複合函式的高階偏導數 習題9.4 9.5 隱函式的微分法 9.5.1 一個方程確定的隱函式 9.5.2 方程組確定的隱函式 習題9.5 9.6 方嚮導數與梯度 9...
習題7-67.7 方嚮導數與梯度習題7-77.8 多元函式的極值及其求法習題7-8本章小結綜合習題7第8章 重積分8.1 二重積分的概念與性質習題8-1...
2偏導數與全微分 3方嚮導數與梯度 4泰勒展開 5雅可比陣 6函式方程組的牛頓-雷夫遜方法 7隱函式 8曲面的切平面 9坐標變換下的微分表達式 10極值與約束極值 11重...
3.2 多元函式的偏導數與全微分3.3 方嚮導數與梯度3.4 多元函式的極值問題3.5 多元函式微分學在幾何上的簡單套用3.6 空間曲線的曲率與撓率3.7 多元向量值函式...
9.4 方嚮導數與梯度 9.4.1 方嚮導數 9.4.2 梯度 習題9.4(A) 習題9.4(B) 9.5 微分法在幾何上的套用 9.5.1 空間曲線的切線與法平面 9.5.2 空間...
8.6方嚮導數與梯度968.6.1方嚮導數968.6.2梯度99習題8.61008.7多元函式微分法在幾何上的套用1018.7.1空間曲線的切線與法平面1018.7.2空間曲面的切平面與法線...
第七節 方嚮導數與梯度第八節 多元函式的極值及其求法第九節 二元函式的泰勒公式第十節 最小二乘法(略)本章知識結構及內容小結...
題型9 方嚮導數與梯度205題型10 二元函式的極值或最值206四、重點題解答208五、同步訓練與提高211參考答案與提示213六、考研真題與解答214...
《高等數學解題方法技巧歸納(下冊·第2版)》實例多、類型廣、梯度大。例題主要...9.8 方嚮導數與梯度9.9 多元函式微分學的幾何套用9.10 二(多)元函式的極...
一、方嚮導數二、梯度 習題6-6第七節 多元函式微分學的幾何套用一、空間曲線的切線與法平面二、曲面的切平面與法線三、等量面與等高線 習題6-7...
第七節 方嚮導數與梯度 第八節 多元函式的極值及其求法 第九節 二元函式的泰勒公式 第十節 最小二乘法 總習題九 第十章 重積分 第一節 二重積分的概念與性...
第六節 方嚮導數與梯度 第七節 多元函式微分學的幾何套用 第八節 多元函式微分學在最大值、最小值問題中的套用 第六章複習題 第七章 重積分 第一節 二重積...
導數與微分、微分中值定理與導數的套用、不定積分、定積分及其套用、微分方程等...第七節 方嚮導數與梯度 第八節 多元函式的極值及其求法 ∗第九節 二元函式...
習題9.69.7方嚮導數與梯度9.7.1方嚮導數9.7.2梯度習題9.79.8二元函式的泰勒公式習題9.89.9多元函式的極值及其求法9.9.1多元函式的極值及最大值、最小值...
8.6 方嚮導數和梯度 628.6.1 基本要求 628.6.2 答疑解惑 628.6.3 基本題型分析 638.6.4 習題全解 658.7?多元函式的極值及套用 678.7.1 基本要求 67...
