基本介紹
- 中文名:點斜式方程
- 外文名:point slope form
- 領域:解析幾何
- 形式:y-y1=k(x-x1)
方程含義
 點斜式方程
點斜式方程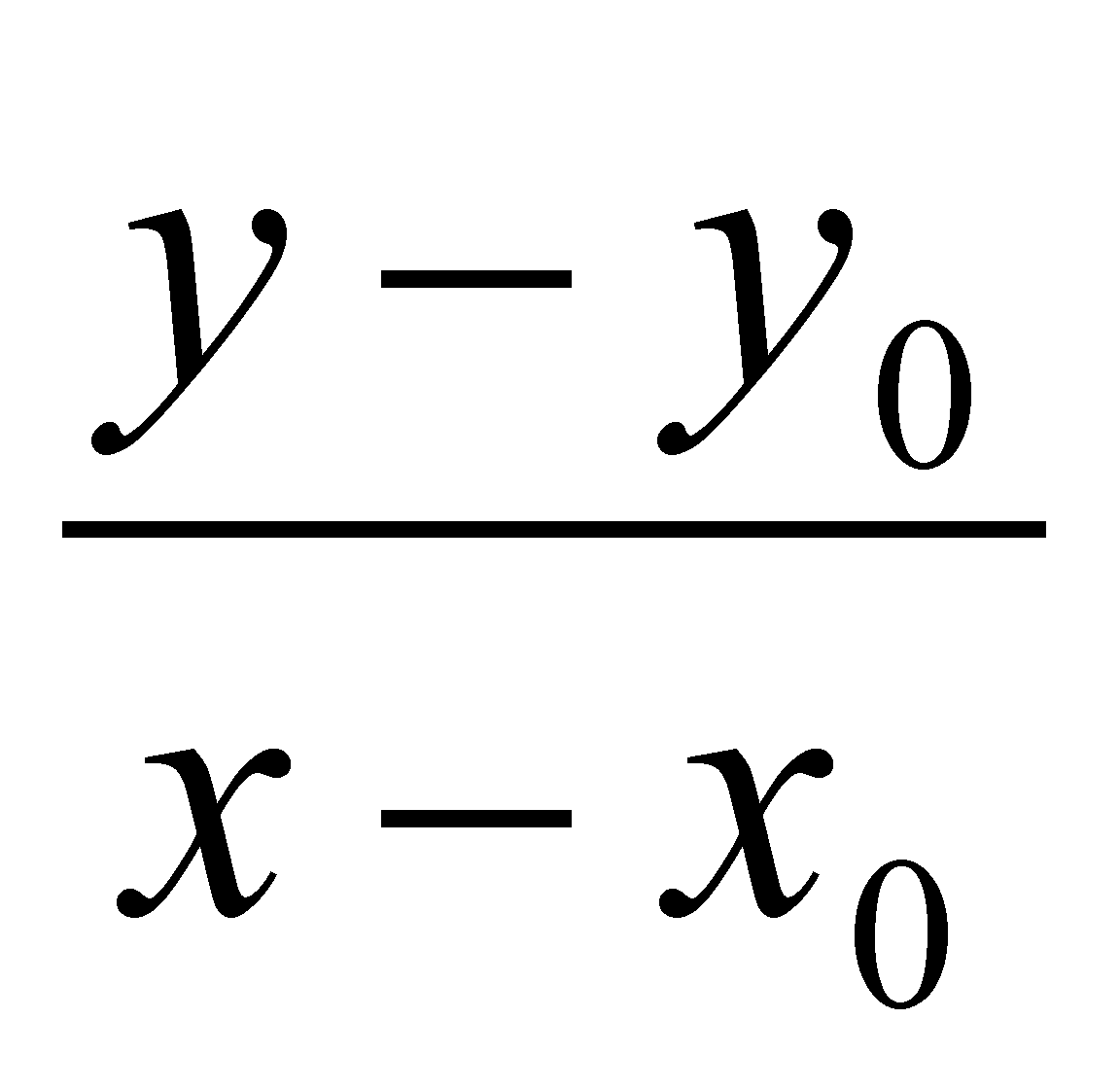
 點斜式方程
點斜式方程點斜式方程是通過直線過的一個點和其斜率求該直線平面方程的一種方法。在平時做解析幾何的題目時,會更多地運用點斜式方程來解題,直接的體現直線的性質。除此之外...
點斜式是指一種算式,已知直線上一點(a,b)並且存在直線的斜率k,則直線可表示y-b=k(x-a)。點斜式方程是通過直線過的一個點和其斜率求該直線平面方程的一...
直線的斜截式方程:y=kx+b,其中k是直線的斜率,b是直線在y軸上的截距。該方程叫做直線的斜截式方程,簡稱斜截式。此斜截式類似於一次函式的表達式。...
5.3 直線的方程 5.3.1 直線的點斜式方程 5.3.2 直線的兩點式方程 5.3.3 直線的一般式方程 5.4 習題課2 5.5 直線的交點 5.5.1 兩條直線的交點 5...
8.1直線方程938.1.1直線的點向式方程938.1.2直線的點法式方程958.1.3直線的斜率978.1.4直線的點斜式方程988.1.5直線的一般式方程100...
5.3 直線的方程 5.3.1 直線的點斜式方程 5.3.2 直線的兩點式方程 5.3.3 直線的一般式方程 5.4 習題課2 5.5 直線的交點 5.5.1 兩條直線...
3.2 直線的方程3.2.1 直線的點斜式方程3.2.2 直線的兩點式方程3.2.3 直線的一般式方程3.3 直線的交點坐標與距離公式3.3.1 兩條直線的交點坐標...
199/3.2 直線的方程199/3.2.1 直線的點斜式方程357/教材習題答案與解析208/3.2.2 直線的兩點式方程357/教材習題答案與解析...
3.2.1直線的點斜式方程 訓練導航 知識精析 基礎鞏固題組 綜合創新題組 解題規律總結 基礎過關訓練 3.2.2直線的兩點式方程 訓練導航 知識精析 ...
7.2 宜線的方程69 7.2.1 直線的傾斜角與斜率69 7.2.2 直線的點斜式方程與斜截式方程72 7.2.3 直線的一般式方程76 7.3 兩條直線的位置關係78...
第一節一次函式與直線 一、 兩個重要公式 二、 直線方程 三、 直線的傾斜角、斜率和截距 習題 2 1第二節直線的方程 一、 直線的點斜式方程 二、 直線的斜...
文化基礎課系列教材:數學(第2冊)》內容分為三角函式、直線和圓的方程、數列、...6.2.2 直線的點斜式方程和斜截式方程 6.2.3 直線的一般式方程 6.3 兩...
