基本介紹
- 中文名:拋物線方程
- 外文名:parabolic equation
- 套用學科:數學
- 適用領域範圍:數學、物理、建築學等
- 解釋:指拋物線的軌跡方程
定義
方程
標準方程 | y^2=2px(p>0) | y^2=-2px(p>0) | x^2=2py(p>0) | x^2=-2py(p>0) |
圖形 |  |  |  |  |
範圍 | x≥0,y  | x≤0,y  | y≥0,x  | y≤0,x  |
對稱軸 | X軸 | y軸 | ||
頂點坐標 | 原點O(0,0) | |||
焦點坐標 | (  | ( 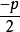 | (0,  | (0,  |
準線方程 |  |  |  | 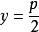 |
離心率 | e = 1 | |||
焦半徑 |  | 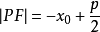 | 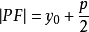 | 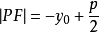 |


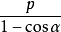
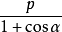
幾何性質
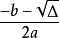

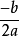

標準方程 | y^2=2px(p>0) | y^2=-2px(p>0) | x^2=2py(p>0) | x^2=-2py(p>0) |
圖形 |  |  |  |  |
範圍 | x≥0,y  | x≤0,y  | y≥0,x  | y≤0,x  |
對稱軸 | X軸 | y軸 | ||
頂點坐標 | 原點O(0,0) | |||
焦點坐標 | (  | ( 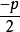 | (0,  | (0,  |
準線方程 |  |  |  | 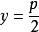 |
離心率 | e = 1 | |||
焦半徑 |  | 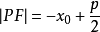 | 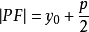 | 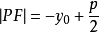 |


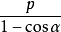
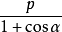
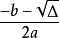

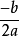
拋物線方程是指拋物線的軌跡方程,是一種用方程來表示拋物線的方法。在幾何平面上可以根據拋物線的方程畫出拋物線。拋物線在合適的坐標變換下,也可看成二次函式圖像。...
平面內,到定點與定直線的距離相等的點的軌跡叫做拋物線。其中定點叫拋物線的焦點,定直線叫拋物線的準線。拋物線是指平面內到一個定點F(焦點)和一條定直線l(準線)...
在直角坐標系中,如果某曲線C上的點與一個二元方程f(x,y)=0的實數解建立了如下的關係:(1)曲線上點的坐標都是這個方程的解;(2)以這個方程的解為坐標的點...
拋物線旋轉方程指的是將拋物線y=ax^2+bx+c(a≠0)繞原點旋轉θ後得到的x、y的方程。該方程的提出者是一名中學生。...
簡稱拋物型方程,一類重要的偏微分方程。熱傳導方程是最簡單的一種拋物型方程。 熱傳導方程研究熱傳導過程的一個簡單數學模型。根據熱量守恆定律和傅立葉熱傳導實驗...
拋物線拱(parabolic arch)是幾何學術語,指工程建築上常用的一種拱形,例如橋拱,它的拱軸線比較理想的是採用懸鏈線y=a(ex/a+e-x/a)/2,拋物線只是它的一種近似...
雙曲線的標準方程編輯 鎖定 討論999 本詞條由“科普中國”科學百科詞條編寫與套用工作項目 審核。雙曲線(Hyperbola)是指與平面上到兩個定點的距離之差的絕對值為...
拋物線法(parabolic approximate method)又稱二次插值法。用二次插值函式逼近未知函式而求解問題的方法。在結構最佳化方面系利用搜尋 區間內三個點的坐標和函式值構造二...
參數曲線即用參數方程表示的曲線,參數方程和函式很相似:它們都是由一些在指定的集的數,稱為參數或自變數,以決定因變數的結果。例如在運動學,參數通常是“時間”...
中的坐標基向量為 ,我們可以將曲線的參數方程寫成向量方程:式中 代表曲線上點的位置向量。稱為關於變數 的向量函式,常簡寫成分量表示 。空間...
多項式變換適用於多項式方程的變換。例如,對拋物線方程 ,令 ,則有曲線相關相關指數 編輯 由相關係數的含義可知,相關係數用於測度現象間線性相關程度的大小。而對於...
數學函式曲線的一種,一條平面代數曲線,顯然, 它和一般的直線都相交三個點。在牛頓之前,也沒有人能夠像把非退化二次曲線分成橢圓、雙曲線與拋物線那樣對三次曲線...
圓橢圓雙曲線拋物線阿基米德螺旋曲線四葉草曲線...... 編輯 數學曲線圓 直角坐標系標準方程:點O(a,b)為圓心,r為半徑,(x-a)^2+(y-b)^2=r^2。極...
本文介紹一個公式,可以簡捷準確地求出直線被拋物線截得的弦長,還可以利用它來判斷直線與拋物線位置關係及解決一些與弦長有關的題目。方法簡單明了,以供參考。 ...
在直角坐標系中,如果某曲線C(看作點的集合或適合某種條件的點的軌跡)上的點與一個二元方程f(x,y)=0的實數解建立了如下的關係:(1)曲線上點的坐標都是這個...
對於直線,法線是它的垂線;對於一般的平面曲線,法線就是切線的垂線;對於空間圖形,是垂直平面。中文名 法線方程 定義 法線斜率與切線斜率乘積為-1 公式 α*β=...
二次函式(quadratic function)的基本表示形式為y=ax²+bx+c(a≠0)。二次函式最高次必須為二次, 二次函式的圖像是一條對稱軸與y軸平行或重合於y軸的拋物線...
拋物線為二次函式的曲線,可以認為是一次函式的曲線即直線的推廣。兩點確定一直線的性質,推廣到拋物線為三點確定一拋物線。...
