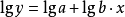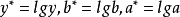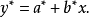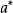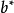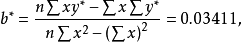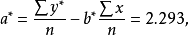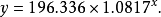曲線相關與曲線回歸分析的含義
曲線相關是相對於線性相關而言的,也稱為非線性相關,即相關的現象之間的相關形式並不表現為直線的關係,而是近似於某種曲線的關係。社會經濟領域有許多現象之間的關係表現為非線性相關。對非線性相關的現象之間的回歸分析稱為非線性回歸分析,或曲線回歸分析。在只涉及一個自變數的情況下,稱兩個變數之間的回歸為一元非線性回歸。非線性回歸分析必須著重解決以下兩個問題:第一,如何確定非線性函式的具體形式。
與線性回歸分析的場合不同,非線性回歸函式有多種多樣的具體形式,需要根據所要研究的問題的性質並結合實際的樣本觀測值做出恰當的選擇。第二。如何估計函式中的參數。非線性回歸分析最常用的方法仍然是
最小二乘估計法。但需要根據函式的不同類型做出適當的處理。
曲線回歸方程的主要函式形式
拋物線形
回歸方程為:
雙曲線形
冪函式曲線
若
和
都接近等比變化,可配合
冪函式曲線。其方程為
指數曲線
對數曲線
曲線回歸方程的線性變換
一元非線性回歸的問題,大多可以轉化為線性回歸問題來解決,也就是通過對非線性回歸模型進行適當的變數變換,使其轉化為線性模型來求解。以下介紹幾種常用的線性變換方法。
倒數變換
倒數變換是用新的變數來替換原模型中變數的倒數,從而使模型變成線性模型的一種方法。例如,對於雙曲線函式,令
代人原方程式,則有
對數變換
對數變換主要用於對數函式的線性變換。對於對數函式,令
,代人原方程,可得
對原方程兩邊取對數
多項式變換
多項式變換適用於多項式方程的變換。例如,對拋物線方程
,令
,則有
相關指數
由相關係數的含義可知,相關係數用於測度現象間線性相關程度的大小。而對於變數之間存在曲線相關的強弱,難以用單相關係數去作正確的判斷。在這種場合下,可以利用相關指數,作為判斷變數之間是否存在某種類型的非線性相關關係的尺度。所謂相關指數,也就是對非線性回歸模型進行擬合時所得到的可決係數。相關指數用R表示,其公式如下:
例題解析
已知某種產品使用壽命與加工溫度的一組數據如表1所示。試配合一條回歸曲線。
加工溫度(℃) | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
使用壽命(小時) | 242 | 250 | 260 | 280 | 310 | 335 | 370 | 415 |
解:從散點圖(見圖1)可以看出,產品的使用壽命與加工溫度的關係近似地表現為一條指數曲線:
。
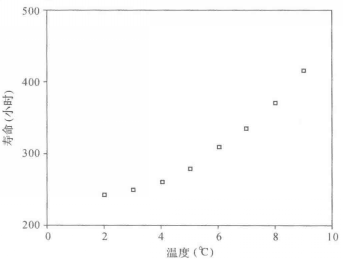 圖1 某產品使用壽命與加工溫度散點圖
圖1 某產品使用壽命與加工溫度散點圖 按直線回歸的方法求參數
及
,計算結果如表2所示。
序號 | x | y* | x2 | xy* |
1 | 2 | 2.3838 | 4 | 4.76763 |
2 | 3 | 2.3979 | 9 | 4.19382 |
3 | 4 | 2.4150 | 16 | 9.65989 |
4 | 5 | 2.4472 | 25 | 12.23579 |
5 | 6 | 2.4914 | 36 | 14.94817 |
6 | 7 | 2.5250 | 49 | 17.67531 |
7 | 8 | 2.5682 | 64 | 20.54561 |
8 | 9 | 2.6180 | 81 | 23.56243 |
合計 | 44 | 19.84654 | 284 | 110.58866 |
所以,產品壽命對加工溫度的曲線回歸方程為
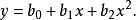
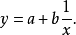
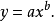
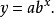
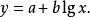
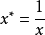
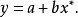

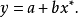
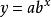
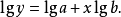
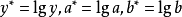

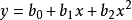
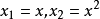
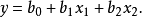

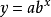
 圖1 某產品使用壽命與加工溫度散點圖
圖1 某產品使用壽命與加工溫度散點圖