基本介紹
曲線列表,曲線介紹,圓,橢圓,雙曲線,拋物線,阿基米德螺旋曲線,四葉草曲線,克萊曲線,
曲線列表
指數函式曲線
曲線介紹
圓
直角坐標系標準方程:點O(a,b)為圓心,r為半徑,(x-a)^2+(y-b)^2=r^2。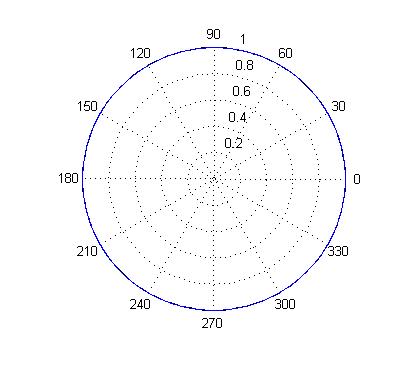

極坐標系標準方程:ρ=r(常量)或者ρ=e*p/(1-e*cos(θ))。(e=0)。
面積公式:S=π*r^2
周長公式:L=2*π*r
橢圓
面積公式:S=π*a*b(a,b分別是長半軸,短半軸的長)。
周長公式:

雙曲線
直角坐標系標準方程:x^2/a^2-y^2/b^2=1極坐標系標準方程:ρ=e*p/(1-e*cos(θ))。(e>1)

面積公式:曲線為開放曲線,無封閉部分
周長公式:曲線為開放曲線
拋物線
直角坐標系標準方程:y^2=2*p*x(x>=0)極坐標系標準方程:ρ=p/(1-cos(θ))或ρ=e*p/(1-e*cos(θ))(e=1)

面積公式:曲線為開放曲線,無封閉部分
周長公式:曲線為開放曲線
阿基米德螺旋曲線
直角坐標系方程:暫無極坐標系方程:ρ=a*θ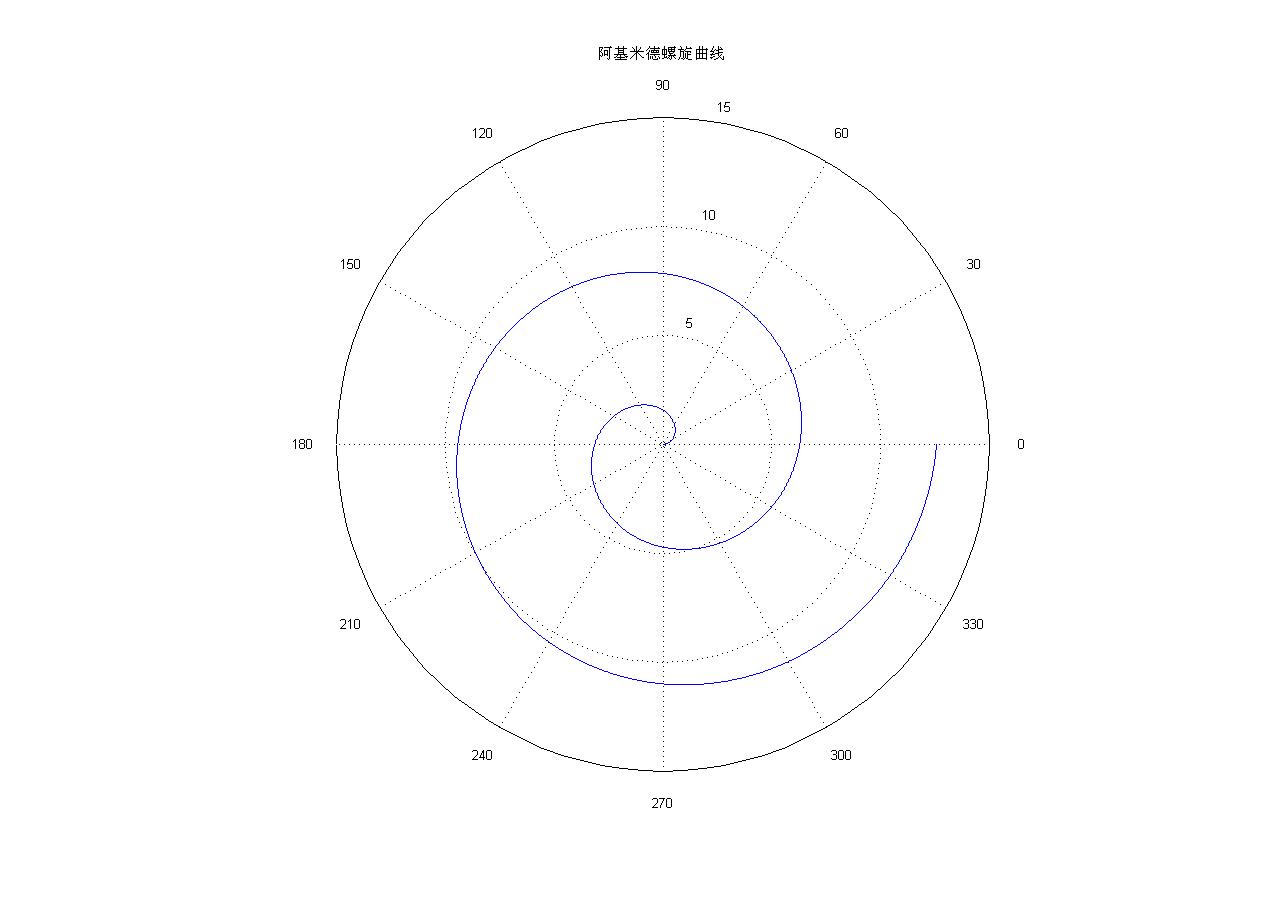

面積公式:暫無
周長公式:暫無
熱門詞條

