發現土星衛星的天文學家喬凡尼卡西尼對把卵形線描繪成軌道有興趣。像笛卡爾卵形線一樣, 笛卡爾卵形線 的作法也是基於對橢圓的針線 作法作修改,從而產生更多的卵形曲線。卡西尼卵形線是由下列條件所定義的:曲線上所有點到兩定點(焦點)的距離之積為常數。
基本介紹
- 中文名:卡西尼卵形線
- 提出者:喬凡尼卡西尼
- P點軌跡:P和焦點的距離的積為常數
- 基礎:橢圓
定義

圖像


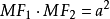
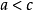
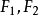

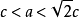


直角坐標方程
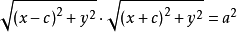
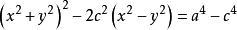



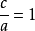
性質
對稱性



極值
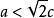
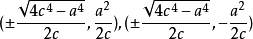


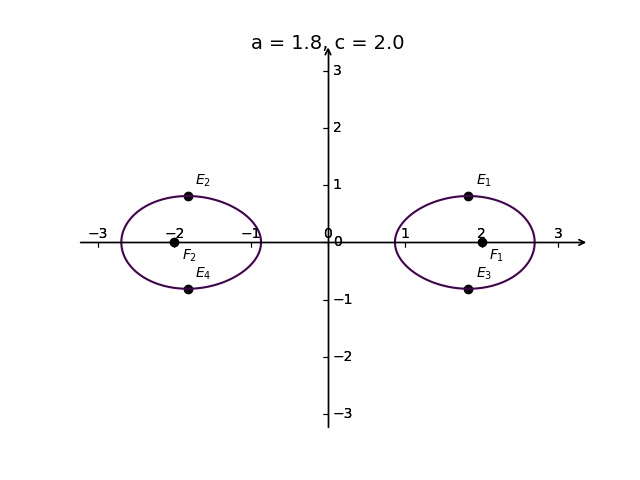
極值點的幾何性質


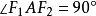

發現土星衛星的天文學家喬凡尼卡西尼對把卵形線描繪成軌道有興趣。像笛卡爾卵形線一樣, 笛卡爾卵形線 的作法也是基於對橢圓的針線 作法作修改,從而產生更多的卵形曲線。卡西尼卵形線是由下列條件所定義的:曲線上所有點到兩定點(焦點)的距離之積為常數。



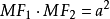
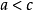
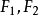

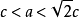


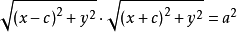
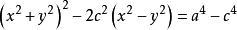



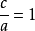



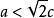
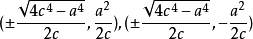





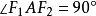

發現土星衛星的天文學家喬凡尼卡西尼對把卵形線描繪成軌道有興趣。像笛卡爾卵形線一樣, 笛卡爾卵形線 的作法也是基於對橢圓的針線 作法作修改,從而產生更多的卵形...
卵形線是類似於橢圓,但是一頭大,一頭小,有一條對稱軸且光滑封閉的平面曲線。卵形線的對稱軸與大、小頭的兩個交點稱為卵形線的大端點和小端點,卵形線上到...
笛卡兒卵形線(Cartesian oval),數學專業術語,是一種典型的卵形線,它一般是一種四次曲線。假定P點與二定點F1與F2的距離分別為r1與r2,它們滿足方程:m*r1+n*r2...
孟格爾卵形線是一種特殊曲線,指極坐標方程是p=2acosnB的曲線,式中n為正整數。...... 發現土星衛星的天文學家喬凡尼卡西尼對把卵形線描繪成軌道有興趣。像笛卡爾...
G.D.卡西尼在理論上是保守的,是最後一位不願接受哥白尼理論的著名天文學家。他反對克卜勒定律,認為行星運動的軌道不是橢圓而是一種卵形線,即卡西尼卵形線──到...
1683年,通過測量巴黎的子午線,得出地球略呈扁長狀的結論(稱“卡西尼卵形線”)。為英國皇家學會會員。著有《已被證實的天文學原理》等。 [1] ...
蛋圓曲線指的是正劈錐面被平面所截得的交線的投影即為平面蛋圓曲線,方程式為...(1)卡西尼卵形線 ,《數學手冊》高等教育出版社1979年5月第一版,392頁。與二...
雞蛋是一個旋轉體,雞蛋殼作為旋轉曲面,使我們想到其截面可近似看作橢圓或卵形線(笛卡爾卵形線、卡西尼卵形線),在蛋殼上任意兩點間用一條細線繃緊,便得到兩點間...
卡西尼卵形線擺線(外擺線、內擺線)懸鏈線玫瑰線心臟線蝴蝶曲線貝塞爾曲線(又稱貝茲曲線,或貝濟埃曲線)貝特朗曲線擬合曲線數學曲線曲線介紹 編輯 ...
雞蛋是一個旋轉體,雞蛋殼作為旋轉曲面,使我們想到其截面可近似看作橢圓或卵形線(笛卡爾卵形線、卡西尼卵形線),在蛋殼上任意兩點間用一條細線繃緊,便得到兩點間...
