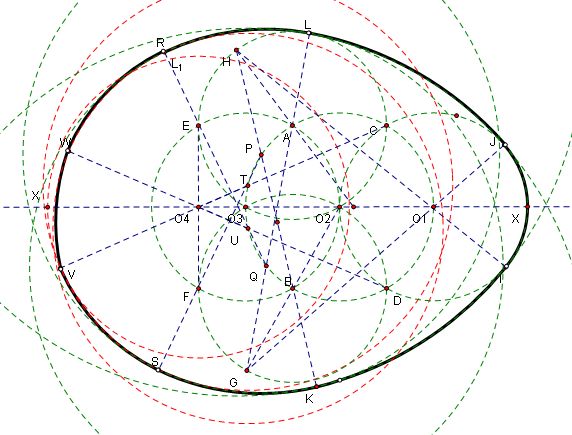
蛋圓曲線指的是正劈錐面被平面所截得的交線的投影即為平面蛋圓曲線,方程式為 x^2/a^2 + y^2 / (ky + b)^2 = 1, 絕對值k小於1,平面上至少有一條對稱軸的卵形曲線是蛋圓曲線。
基本介紹
- 中文名:蛋圓曲線
- 實質:交線投影
- 方程式:x^2/a^2 + y^2 / (ky + b)^2 = 1
- 形狀:類似於蛋圓形
定義,劈錐曲線族,公式,注釋,
定義
平面上至少有一條對稱軸的卵形曲線是蛋圓曲線。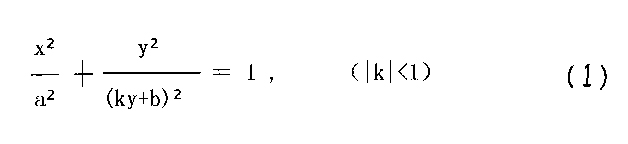
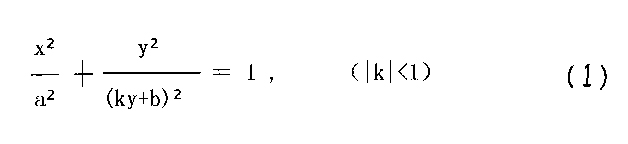
劈錐曲線族
本文涉及的蛋圓屬於劈錐曲線族,是四次方程曲線。在橢圓方程中,令a = b = r ,橢圓即成為特例——圓;而橢圓又是蛋圓的一種特例。
公式
設準線為橢圓的正劈錐面方程為 x^2 / a^2 + y^2 / z^2 = 1,其軸為 x 軸,準線為 x^2 / a^2 + y^2 / b^2 = 1,以平行於劈錐面軸的平面
z = ky + b 去截正劈錐面,得交線為 x^2 / a^2 + y^2 / b^2 = 1
{ z = ky + b (2),將(2)投影到 xOy 平面上,即得蛋圓標準方程(1),見圖1。
仿橢圓參數方程,引入角參數 t ,蛋圓參數方程為
{ x = a cos t
y = b sin t / ( 1-k sin t) (∣k∣﹤1) (3)。令(1)在三維直角坐標系中繞 y 軸旋轉,得出旋轉蛋球面方程(詳見圖2):

蛋圓(1)的取值範圍:a > 0, b > 0, ︱k︱< 1。
因為 k 是平面 ky + b 對於 zOx 坐標面的斜率,︱k︱﹥ 1時,平面在正劈錐面上不能截到封閉的卵形線,k = 0 時(1)成為特例——橢圓。b = 0 時(1)成為兩條直線: —a ≤ x ≤ a ;
-b / (1 + k) ≤ y ≤ b / (1 - k)。
蛋圓(1)內線段:(1)與 x 軸兩個交點的連線線段稱“橫徑”,其長度記為 2r,橫徑被其中點所分成的兩個線段稱“對稱半徑”,其長度記為r ,r = a ;(1)以 y 軸為唯一對稱軸,是偶函式,(1)與其對稱軸的兩個交點間的線段稱“直徑”,其長度記為 d ,
d = b / (1-k) - [-b/ (1 + k )] = 2b /(1-k^2);直徑與橫徑的比值稱圓度記為u,u = d / 2r = b / a(1-k^2),當u = 1時蛋圓變為特例——圓,當u → 0 時蛋圓越來越矮胖,當u →∞時蛋圓越來越瘦長。
由於蛋圓(1)是已知唯一的三參數蛋圓曲線,調節a、b、k三個參數比例,可以無限逼近符合定義的任何蛋圓,包括獲得比橢圓方程式更精確地逼近真實的地球外形方程式。
圖3:計算機繪製的立體蛋圓——蛋球面
(方程式為:(x^2 + z^2) /16 + y^2/(0.2y +5)^2= 1)
圖4:上海世博文化中心(從模型紀念品可見其俯視圖為平面蛋圓曲線) 圖3:蛋球面
圖3:蛋球面
 圖3:蛋球面
圖3:蛋球面 圖4:上海世博文化中心立體圖
圖4:上海世博文化中心立體圖注釋
注1 卵形線定義:平面上與任一直線相交不多於兩點的閉曲線。它是凸閉曲線。
《數學詞典》215頁,上海辭書出版社1992年8月第一版。
注2 本文主要引用《淺析橢圓的一種推廣——蛋圓》曹明建、曹明達1999-09-01。
注3 國內課題來源:《科學畫報》1983.6,36頁《怎樣畫蛋》王根明、陸彤,“用數學術語來表示蛋的形態曲線,至今還沒有研究出來。”(第8行)
注4 國際課題來源:英國《新科學家》29july1982,Vol95,No1316,P290 <<The drawing-out of an egg>>,Robert Dixon,P293末段。
注5 蛋圓套用介紹:(1)《知識窗》1995.11,25頁,《蛋形的奧秘》曹明建、王令朝。(2)《科學畫報》1996.11,13頁《蛋形的魅力》王令朝,本文披露了蛋圓標準方程,可惜方程式在逗號前漏印了“= 1”。(3)《文匯報》2008.07.29.11版《師法自然賦流形(上)》詹克明,整個第二節討論“師法蛋殼力學特徵的穹頂結構”。
注6 其他蛋圓
(1)卡西尼卵形線 ,《數學手冊》高等教育出版社1979年5月第一版,392頁。與二定點的距離之積為常數的動點軌跡,
( x^2 + y^2)^2- 2c^2(x^2-y^2) = a^4 -c^4 (a < c)
(2)《數學通報》1995.7,36頁《關於超圓、超球等幾何圖形面、體積的計算》張正印,x^2 + y^2 = (y a^1/n )^[2n/(n+1)],(a>0,n>0)
(3)《形形色色的曲線》178頁,孟格爾卵形線ρ= 2a cos ^n θ ,
N 為正整數。蔣聲編著,屬於《中學生文庫精選續編·數學趣談輯》,上海教育出版社1999年12月第2版。