皮亞諾曲線(Peano curve)是一曲線序列的極限。只要恰當選擇函式,畫出一條連續的參數曲線,當參數t在0、1區間取值時,皮亞諾曲線將遍歷單位正方形中所有的點,得到一條充滿空間的曲線。 皮亞諾曲線是一條連續而不可導的曲線。
基本介紹
- 中文名:皮亞諾曲線
- 外文名:Peano curve
- 提出者:朱塞佩•皮亞諾
- 原像維度:1維
- 像的維度:2維
- 性質:曲線的像充滿正方形
皮亞諾曲線的發現


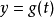
 皮亞諾曲線
皮亞諾曲線維數的認識
集合論觀點











皮亞諾曲線(Peano curve)是一曲線序列的極限。只要恰當選擇函式,畫出一條連續的參數曲線,當參數t在0、1區間取值時,皮亞諾曲線將遍歷單位正方形中所有的點,得到一條充滿空間的曲線。 皮亞諾曲線是一條連續而不可導的曲線。


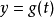
 皮亞諾曲線
皮亞諾曲線









皮亞諾曲線(Peano curve)是一曲線序列的極限。只要恰當選擇函式,畫出一條連續的參數曲線,當參數t在0、1區間取值時,皮亞諾曲線將遍歷單位正方形中所有的點,得到...
1890年,義大利數學家皮亞諾(Peano G)發明能填滿一個正方形的曲線,叫做皮亞諾曲線。後來,由希爾伯特作出了這條曲線,又名希爾伯特曲線。皮亞諾對區間[0,1]上的...
1890年,義大利數學家皮亞諾(G.Peano)構造了填充空間的曲線。該曲線即為Peano填充曲線。...
朱塞佩·皮亞諾 Giuseppe Peano (1858年8月27日 - 1932年4月20日) 是義大利數學家、邏輯學家、語言學家。生於斯賓尼塔,卒於都靈。他大多數生涯在義大利的...
數學曲線曲線列表 編輯 三角函式曲線(正弦函式,餘弦函式,正切函式,餘切函式,正割函式,餘割函式)指數函式曲線擺線(旋輪線圓滾線)皮亞諾曲線科克曲線...
“禪師體”,一種於2012年7月在社交網站上流行起來的文體,受到廣大學術青年、偽學術青年們的追捧。如:莫比斯環只有一面;皮亞諾曲線可以遍歷單位正方形中所有的點...
從皮亞諾曲線引起的維數及連續統的研究,習慣上也看成一般拓撲學的分支。拓撲學代數拓撲 L.E.J.布勞威爾在1910~1912年間提出了用單純映射逼近連續映射的方法, ...
孟德伯顯示計算它們的豪斯道夫維度的方法,它們的維度都是1和2之間。他亦提及填滿空間、維度為2的皮亞諾曲線,但並未給出其構造。...
從皮亞諾曲線引起的維數及連續統的研究,習慣上也看成一般拓撲學的分支。 [1] 點集拓撲學簡介 編輯 拓撲學是把那些很樸素但又很基本的圖形的集和直觀性質,...
2.12 皮亞諾曲線 2.13 雪花曲線 2.14 謝爾賓斯基的奇妙圖形 2.15 英國的海岸線有多長 第三章 微積分悖論 3.1 芝諾悖論 3.2 德謨克利特悖論 3.3 克卜勒的...
一、科赫曲線 156二、康托爾集 156三、皮亞諾曲線 157四、謝爾賓斯基襯墊、地毯、海綿 157五、維數與分維 159六、分形圖是高效率的 161第三節美麗的蝴蝶 162...
[1] 在《內蘊幾何學教程》中給出了皮亞諾曲線函式的解析形式,得到了“切薩羅曲線”等結果,並在一般形式下討論了曲面和多維空間的性質。[1] 他的著作還涉及...
嘉當引進了“濾子”的概念,能進一步刻畫一致收斂,使收斂的更本質的屬性揭示了出來;維數的問題是E.嘉當在研究皮亞諾曲線(一種可填滿整個正方形的“曲線”)時提出...
1.L6明可夫斯基香腸1.1.7 皮亞諾曲線1.1.8 謝爾賓斯基三角墊1.1.9 謝爾賓斯基方毯1.1.1 0門格爾海綿1.2 分形幾何的定義1.2.1 Mandelbrot的定義...
1872年,魏爾斯特拉斯給出了第一個處處連續但處處不可微函式的例子,使人們意識到連續性與可微性的差異,由此引出了一系列諸如皮亞諾曲線等反常性態的函式的研究...
通過對分形理論的深入研究,證明了皮亞諾曲線的一些性質,尤其對Hilbert空間填(略),為空間索引的研究提供了必要的理論知識。 [1] 空間數據(略)空間信息領域的核心...
4.3 皮亞諾曲線與希爾伯特曲線4.4 柯赫曲線4.5 謝爾賓斯基地毯第五章 林氏系統與疊代函式系統5.1 林氏系統5.2 實例與偽碼5.3 供實驗的林氏系統數據表5.4 疊代...
§27.4 二維連續統概念、一般曲線概念 §27.5 覆蓋整個正方形的皮亞諾曲線 §27.6 較狹義的曲線概念:若當曲線 §27.7 更狹義的曲線概念:正則曲線 §27.8...
§4.6 約當曲線、皮亞諾曲線、可求長曲線內容小結與例題選講複習題四第五章 可測函式§5.1 廣義實函式與逆象型集合§5.2 可測函式的概念及其性質...
