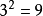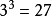數學家豪斯道夫(Hausdorff)在1919年提出了連續空間的概念,也就是空間維數是可以連續變化的,它可以是整數也可以是分數,稱為豪斯道夫維數。記作Df,一般的表達式為:K=L^Df,也作K=(1/L)^(-Df),取對數並整理得Df=lnK/lnL,其中L為某客體沿其每個獨立方向皆擴大的倍數,K為得到的新客體為原客體的比例係數。顯然,Df在一般情況下是一個分數。因此,曼德布羅特也把分形定義為豪斯道夫維數大於或等於拓撲維數的集合。英國的海岸線為什麼測不準?因為歐氏一維測度與海岸線的維數不一致。根據曼德布羅特的計算,英國海岸線的維數為1.26。有了分維,海岸線的長度就確定了。
分數維度是基於分形理論產生的。由於圖形擁有自相似性,產生了分數維度。

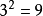

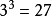
 。l是放大為幾倍。d就是拓撲維。
。l是放大為幾倍。d就是拓撲維。