蔓葉線,有時又叫雙蔓葉線是 Diocle 在公元前180年發現的曲線。
在幾何形狀中,蔓葉線是從兩個給定曲線C1,C2和點O(極點)產生的曲線。
基本介紹
- 中文名:蔓葉線
- 外文名:Cissoid
- 表達式:y^2=x^3/2*a-x(a為常數)
- 提出者:Diocle
- 提出時間:公元前180年
- 套用學科:數學幾何
- 又名:雙蔓葉線
曲線方程,推導,軌跡定義,歷史,
曲線方程
以o為原點,漸近線為x=2a,圓的半徑為a
則蔓葉線的標準曲線方程為:
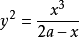
其中a是常數。
推導
取蔓葉線上一點P(x0,y0),直線OP的方程是

它與圓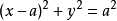 的交點A坐標分別是(x1,y1),其中
的交點A坐標分別是(x1,y1),其中 ,
,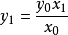 。
。
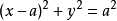

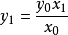
OP與直線x=2a的交點坐標是B(2a, )。則
)。則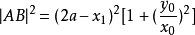 ,且
,且 ,兩者相等,得到
,兩者相等,得到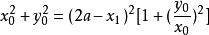 ,整理得
,整理得 ,,再次整理得
,,再次整理得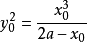 ,這就是P點滿足的方程。
,這就是P點滿足的方程。

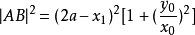

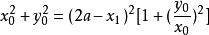

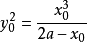
軌跡定義
蔓葉線可以軌跡來定義出來。
假設 C1 和 C2 是兩條曲線, O 是一個定點,一條經過 O 的直線 L 分別相交 C1 和 C2 於 A 和 B,則所有在 L 上的點 P 使得 AB = OP 的軌跡就是一條蔓葉線。

若 C1 為一個圓,C2 是圓的切線,O 是圓上的點且在切線的對面,那么 P 的軌跡就是本頁頂的圖像,稱為「Diocle 蔓葉線」。
歷史
這曲線的發現是為了解決倍立方問題。蔓葉線的英文名字「Cissoid」是曲線發現了100年後《Geminus》中出現的,意為「像常春藤的」。

