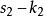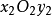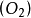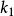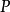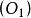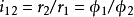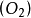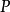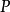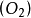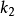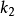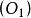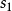如果在兩條曲線之間可以建立一個點對應,使得在對應點這兩條曲線有公共的主法線,則稱這兩條曲線為共軛曲線。
基本介紹
- 中文名:共軛曲線
- 外文名:conjugate curve
- 套用學科:數學術語
- 範疇:數理科學
- 定義:在對應點兩條曲線有公共的主法線
- 涉及:Bertrand曲線
概念,設計共軛曲線機構的圖解法,包絡法,法線法,
概念
如果在兩條曲線之間可以建立一個點對應,使得在對應點這兩條曲線有公共的主法線,則稱這兩條曲線為共軛曲線。如果一條曲線有不與自身重合的共軛曲線,則稱其為Bertrand曲線。互為共軛的曲線 之間距離為常數,且在對應點間的切線成定角。
之間距離為常數,且在對應點間的切線成定角。

設計共軛曲線機構的圖解法
包絡法
 圖1
圖1設 相對
相對 滾動(圖1),其角速度分別為
滾動(圖1),其角速度分別為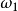 、
、 ,套用反轉法,給整個機構繞
,套用反轉法,給整個機構繞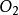 的反轉角速度
的反轉角速度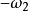 ,則
,則 固定,
固定, 沿
沿 滾動,如圖1表示
滾動,如圖1表示 連同
連同 滾到
滾到 、
、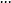 等位置。此時:
等位置。此時: ,與
,與 固結的
固結的 。
。



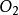
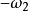






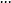



構想 沿
沿 滾動至無數點接觸,相應地有無數條曲線
滾動至無數點接觸,相應地有無數條曲線 、
、 、
、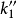 、
、 ,這些
,這些 曲線的包絡線即為曲線
曲線的包絡線即為曲線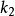 。由此可知,已知
。由此可知,已知 、
、 和共軛曲線
和共軛曲線 、
、 中的一條,可利用包絡原理求出與其共軛的另一條,故共軛曲線機構常稱為包絡線機構。注意圖1中法線
中的一條,可利用包絡原理求出與其共軛的另一條,故共軛曲線機構常稱為包絡線機構。注意圖1中法線 過點
過點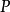 、
、 過點
過點 、
、 ,
, 常值。
常值。




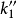
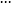

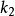





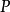




法線法
設給定瞬心線 、
、 的中心距
的中心距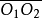 、傳動比
、傳動比 及共軛曲線中的一條曲線
及共軛曲線中的一條曲線 ,求作嚙合線及
,求作嚙合線及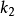 。
。


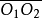


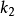
 圖2
圖2如圖2,建立三個坐標系:定坐標系 或
或 ,分別與
,分別與 、
、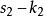 一起轉動的動坐標系
一起轉動的動坐標系 或
或 、
、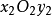 或
或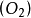 三個坐標的始位相互平行。起始時
三個坐標的始位相互平行。起始時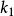 上點
上點 進入嚙合,法線
進入嚙合,法線 過點
過點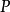 。設
。設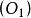 轉過角
轉過角 ,由
,由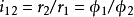 可知
可知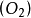 轉過
轉過 ,此時
,此時 轉到圖示的
轉到圖示的 ,
, 的法線
的法線 亦過點
亦過點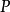 ,故點
,故點 進入嚙合。
進入嚙合。 為嚙合點畫在
為嚙合點畫在 上的軌跡,稱為嚙合線;
上的軌跡,稱為嚙合線; 、
、 、
、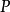 等嚙合點畫在動坐標系
等嚙合點畫在動坐標系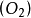 上的軌跡即為所求曲線
上的軌跡即為所求曲線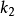 ,圖示
,圖示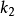 為始位。注意
為始位。注意 等嚙合點畫在
等嚙合點畫在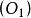 上的軌跡就是曲線
上的軌跡就是曲線 。
。