基本介紹
定義,符號史,基本運算,不盡根數,找到所有方根,解多項式,算法,
定義
如果一個數的n次方(n是大於1的整數)等於a,那么這個數叫做a的n次方根。當n為奇數時,這個數為a的奇次方根;當n為偶數時,這個數為a的偶次方根。
符號史
最早的根號“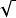 ”源於字母“L”的變形(出自拉丁語latus的首字母,表示“邊長”),沒有線括弧(即被開方數上的橫線),後來數學家笛卡爾給其加上線括弧,但與前面的方根符號是分開的,因此在複雜的式子顯得很亂。直至18世紀中葉,數學家盧貝將前面的方根符號與線括弧一筆寫成,並將根指數寫在根號的左上角,以表示高次方根(當根指數為2時,省略不寫。)。從而,形成了我們現在所熟悉的開方運算符號
”源於字母“L”的變形(出自拉丁語latus的首字母,表示“邊長”),沒有線括弧(即被開方數上的橫線),後來數學家笛卡爾給其加上線括弧,但與前面的方根符號是分開的,因此在複雜的式子顯得很亂。直至18世紀中葉,數學家盧貝將前面的方根符號與線括弧一筆寫成,並將根指數寫在根號的左上角,以表示高次方根(當根指數為2時,省略不寫。)。從而,形成了我們現在所熟悉的開方運算符號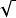 。
。
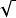
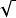
由於在計算機中的輸入問題,我們有時還可以使用sqrt(a,b)來表示a的b次方根。
基本運算
帶有根號的運算由如下公式給出:



對於所有的非零複數a,有n個不同的複數b使得b=a,所以符號 不能無歧義的使用。n次單位根是特別重要的。
不能無歧義的使用。n次單位根是特別重要的。




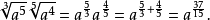



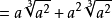

不盡根數
經常簡單的留著數的n次方根不解(就是留著根號)。這些未解的表達式叫做“不盡根數”(surd),它們可以接著被處理為更簡單的形式或被安排相互除。
如下恆等式是操縱不盡根數的基本技術:



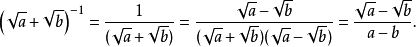
找到所有方根



正實數
所有x=a或a的n次方根,這裡的a是正實數,的複數解由如下簡單等式給出:



解多項式
曾經猜想多項式的所有根可以用根號和基本運算來表達;但是阿貝爾-魯菲尼定理斷言了這不是普遍為真的。例如,方程

算法
對於正數A,可以通過以下算法求得 的值:
的值:

(1)猜一個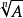 的近似值,將其作為初始值
的近似值,將其作為初始值 ,
,
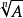

(2)設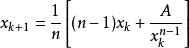 。記誤差為
。記誤差為 ,即
,即 ,
,
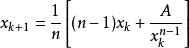


(3)重複步驟2,直至絕對誤差足夠小,即: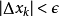 。
。