基本介紹
- 中文名:完全平方式
- 外文名:Perfect square trinomial
- 公式1:a2+2ab+b2=(a+b)2
- 公式2:a2-2ab+b2=(a-b)2
- 相關術語:完全平方數
- 別稱:完全平方公式
定義及公式
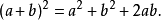
例子




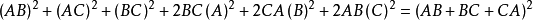


注意

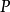









準完全平方式
導言












定義





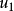


例子




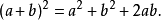




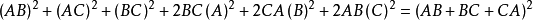



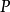


























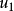





完全平方式是指如果滿足對於一個具有若干個簡單變元的整式A,如果存在另一個實係數整式B,使A=B^2的條件話,則稱A是完全平方式,亦可表示為(a+b)²=a²+...
完全平方指用一個整數乘以自己例如1*1,2*2,3*3等,依此類推。若一個數能表示成某個整數的平方的形式,則稱這個數為完全平方數。完全平方數是非負數,而一個...
《完全平方數及其套用》是2015-8-1出版的圖書,作者是南秀全。...... 介紹了完全平方數的性質以及完全平方數與完全平方式的關係.並介紹了如何判別完全平方數及求解...
完全立方公式包括完全立方和公式和完全立方差公式,完全立方和(或差)公式指的是兩數和(或差)的立方等於這兩個數的立方和(或差)與每一個數的平方乘以另一個數3...
③方程兩邊同時加上一次項係數一半的平方;④把左邊配成一個完全平方式,右邊化為一個常數;⑤進一步通過直接開平方法求出方程的解,如果右邊是非負數,則方程有兩個...
配方法是指將一個式子(包括有理式和超越式)或一個式子的某一部分通過恆等變形化為完全平方式或幾個完全平方式的和,這種方法稱之為配方法。這種方法常常被用到...
對於某些不能利用公式法的多項式,可以將其配成一個完全平方式,然後再利用平方差公式,就能將其因式分解,這種分解因式的方法叫做配方法。屬於拆項、補項法的一種...
個位是5的數的平方把a看作10的個數,這樣個位數字是5的數的平方可以寫成;(10a+5)²的形式。根據完全平方式推導;= ==由此可知:個位數字是5的數的平方,...
該公式的文字表達為:兩數和,乘它們的平方和與它們的積的差,等於這兩個數的...3 完全立方公式 ▪ 分解步驟如下 ▪ 解題時常用它的變形: 4 公式證明...
平方差公式 [2] 。即 立方和(差)公式 [3] 。即 完全立方公式及其變式 [4] 。即 變式。即三數和平方公式。即 多項式平方公式。即(對於四項而言) ...
3. 數學術語。把不完全平方式變為完全平方式。【造句】時間是一枚金幣,每個人都平等地擁有。不懂時間配方的人,也談不上這枚金幣的消費。你打算用你的金幣去買...
把由(5)式求出的y值代入(4)式後,(4)式的兩邊都成為完全平方,兩邊開方,可以得到兩個關於x的一元二次方程。解這兩個一元二次方程,就可以得出原方程的四個...
因式分解中的平方差公式:因式分解中的完全平方公式: ,因式分解中的三數完全平方公式:十字相乘法(Cross Method):運用十字交叉線來分解係數,把二次三項式分解因式的...
把由(5)式求出的y值代入(4)式後,(4)式的兩邊都成為完全平方,兩邊開方,可以得到兩個關於x的一元二次方程。解這兩個一元二次方程,就可以得出原方程的四個...
把a看作10的個數,這樣個位數字是5的數的平方可以寫成;(10a+5)^2的形式。根據完全平方式推導;(10a+5)^2=(10a)^2+2×10a×5+5^2...
