當冪的指數為負數時,稱為“負指數冪”。正數a的-r次冪(r為任何正數)定義為a的r次冪的倒數。
基本介紹
- 中文名:負指數冪
- 外文名:negative exponent
- 所屬學科:數學(代數)
- 相關概念:冪,乘方等
基本介紹
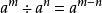
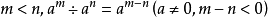
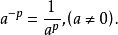
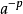
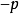

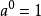
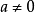
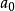
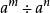
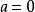
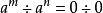
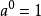
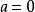
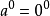
相關概念
冪



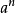

分指數冪




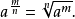
乘方

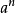


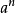
正整數指數冪
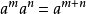
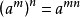
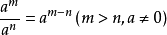
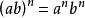
負整數指數冪
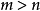
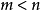
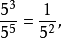
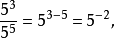
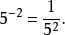
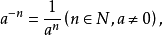
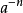
零指數冪
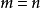

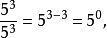
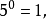

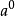
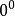
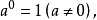
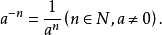
整數指數冪的運算法則
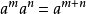
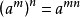
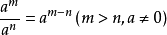
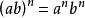
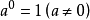
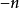
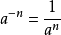
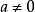

冪的運算法則
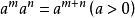
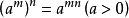
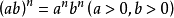

當冪的指數為負數時,稱為“負指數冪”。正數a的-r次冪(r為任何正數)定義為a的r次冪的倒數。
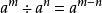
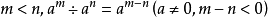
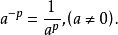
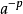
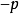

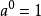
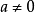
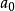
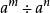
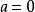
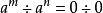
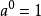
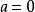
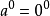



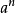





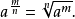

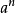


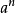
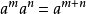
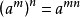
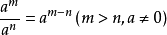
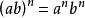
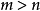
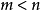
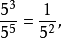
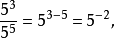
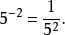
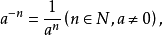
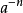
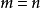

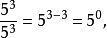
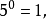

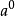
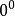
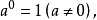
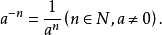
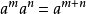
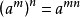
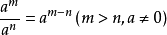
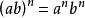
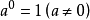
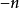
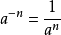
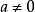

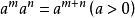
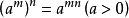
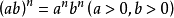
當冪的指數為負數時,稱為“負指數冪”。正數a的-r次冪(r為任何正數)定義為a的r次冪的倒數。...
一般地,在數學上我們把n個相同的因數a相乘的積記做a^n。這種求幾個相同因數的積的運算叫做乘方,乘方的結果叫做冪。在a^n中,a叫做底數,n叫做指數。a^n讀作...
冪運算是一種關於冪的數學運算。同底數冪相乘,底數不變,指數相加。同底數冪相除,底數不變,指數相減。冪的乘方,底數不變,指數相乘。...
形如ax的式子稱為冪,其中a稱為冪的底數,x稱為冪的指數。當x取正整數,零,負整數時,ax分別稱為正整數指數冪、零指數冪、負整數指數冪,統稱為整數指數冪。...
冪負指數冪 有了零指數冪的定義之後,現在來定義負指數冪。當底數n≠0時,由於 ,根據冪的運算規則可知, 。因此定義負指數冪如下:...
指數加減底不變,同底數冪相乘除。 指數相乘底不變,冪的乘方要清楚。 積商乘方原指數,換底乘方再乘除。 非零數的零次冪,常值為 1不糊塗。 負整數的指數冪,...
冪的有關概念 ⑴ 正整數指數冪:a^n=a·a·a…·a﹙n∈N*﹚ ╰──╮╭─╯ n ⑵零指數冪:aº=1﹙a≠0﹚ ⑶負數指數冪:a^-p=1/aˆp(a≠...
實數指數冪基本包括整數指數冪、分數指數冪與無理數指數冪。其一般形式為 a^n (n是實數)...
指數符號(Sign of power)的種類繁多,且記法多樣化。我國魏晉時期數學家劉徽《九章算術注》(263年)內以「冪」字表示指數,一直沿用。我國古代稱【一數自乘」為...
求n個相同因數乘積的運算,叫做乘方,乘方的結果叫做冪(power)。其中,a叫做底數(base number),n叫做指數(exponent)。當aⁿ看作a的n次乘方的結果時,也可讀作“...
