絕對連續表示函式的光滑性質,比連續和一致連續條件都要嚴格,比利普希茨條件寬鬆,是一類極為重要的函式。絕對連續函式幾乎處處可微,是它的導函式的廣義原函式。
基本介紹
- 中文名:絕對連續函式
- 外文名:Absolutely continuous function
- 定義:數學函式
- 詞性:函式名詞
簡介
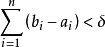

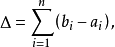
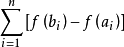
性質
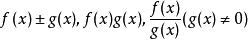
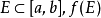


絕對連續表示函式的光滑性質,比連續和一致連續條件都要嚴格,比利普希茨條件寬鬆,是一類極為重要的函式。絕對連續函式幾乎處處可微,是它的導函式的廣義原函式。
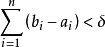

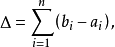
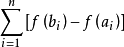
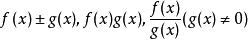
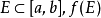

絕對連續表示函式的光滑性質,比連續和一致連續條件都要嚴格,比利普希茨條件寬鬆,是一類極為重要的函式。絕對連續函式幾乎處處可微,是它的導函式的廣義原函式。...
積分一致絕對連續是描述測度空間中一列函式的積分絕對連續的一致性的重要概念。測度空間是定義了測度的可測空間。設(Ω,F)是可測空間,μ是F上的測度,(Ω,F,μ...
半絕對連續函式是絕對連續函式概念的推廣。上、下半絕對連續函式統稱為半絕對連續函式。...
第1章導言,簡單介紹勒貝格測度與勒貝格積分的起源及其基本理念;第2~6章分別為集合、n維歐氏空間、測度論、可測函式、積分論;第7章有界變差函式與絕對連續函式,...
設f(x)是定義在閉區間[a,b]上的實值函式,若存在狹義一般絕對連續函式F(x),使得在區間[a,b]上F'(x)=f(x)幾乎處處收斂,則稱f(x)為[a,b]上的狹義...
有些索博列夫空間有簡單的表述。例如,在一維情況, 就是絕對連續函式空間,而W是李普希茲函式空間。還有, 可以自然地用其傅立葉級數的術語定義,也就是...
平方可積函式空間,即 ,在 上定義運算元 如下:={ 在 絕對連續, },則 。定義運算元顯然有 ⊂ ⊂ 。下面來證明根據這個結果可知 ⊂ ⊂ ,故 是對稱運算元, ...
上滿足李普希茨條件,則該函式在 上必為絕對連續函式。換言之,絕對連續為李普希茨條件之必要條件,而李普希茨條件為絕對連續之充分條件。若...
設f(x)是定義在閉區間[a,b]上的一個實值函式。若存在一般絕對連續函式F(x),使得對於[a,b]中幾乎所有的點,F(x)的近似導數F'ap(x)=f(x),則稱f(x)...
1.2 函式的上極限和下極限1.3 上、下半連續函式§2 弱收斂和弱收斂§3 單位連續分解§4 絕對連續函式§5 幾個緊緻性定理§6 凸集與凸函式...
循著紐曼的途徑,人們發現了許多En(f)與Rn(f)不同階的函式f。...指出,對導數的全變差小於1的絕對連續函式f,有Rn(f)=O(n-2)。由此可以推出...
§4.6絕對連續函式習題4附錄4.1葉戈羅夫生平附錄4.2盧津生平第5章積分§5.1非負簡單函式的積分§5.2非負可測函式的積分§5.3一般可測函式的積分...
積分的性質主要有線性性、保號性、極大值極小值、絕對連續性、絕對值積分等。...反三角函式的積分、含有指數函式的積分、含有對數函式的積分、含有雙曲函式的積分...
設f(x)是定義在閉區間[a,b]上的實值函式,若存在狹義一般絕對連續函式F(x),使得在區間[a,b]上F'(x)=f(x)幾乎處處收斂,則稱f(x)為[a,b]上的狹義...
貝爾(Baire)發表了關於不連續實變函式理論的第一篇論文.這些成功的研究工作說明在這些嶄新的領域中進行開拓將會獲得何等重要的成就,從而激發了勒貝格的熱情.從1899年...
利用有界變差函式成功地刻畫了重要的核空間,解決了多年來許多數學工作者一直未能解決的絕對連續函式與弱絕對連續函式等價的條件,得到了不含C0巴拿赫空間的又一特徵,...
《實分析與泛涵分析》通過改革和創新,用集合(通過引入各種結構)和映射將傳統的“實變函式論”、“測度論”、“泛函分析”三門課融合為一門新的“現代分析”基礎...
