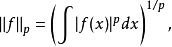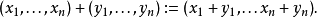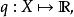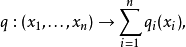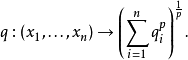簡介
一個向量v乘以一個
標量a時,長度應變為原向量v的|a|(a的
絕對值)倍。
三角不等式成立。也就是說,對於兩個向量v和u,它們的長度和(“
三角形”的兩邊)大於v+u(第三邊)的長度。
一個把向量映射到非負實數的
函式如果滿足以上性質,就叫做一個
半範數;如果只有零向量的函式值是零,那么叫做
範數。擁有一個範數的
向量空間叫做
賦范向量空間,擁有半範數的叫做
半賦范向量空間。
定義
一個半賦范向量空間(E,p)由一個向量空間E以及一個E上的
半範數p構成。
一個賦范向量空間(E,||·||)由一個向量空間E以及一個E上的
範數||·|| 構成。
拓撲結構
設(
E,||·||)是一個賦范向量空間,那么由範數 ||·|| 很自然地定義了一個
拓撲上的
距離:
由此就定義了一個
E上的拓撲結構,稱為範數 ||·||
誘導的自然拓撲。這也是使得函式 ||·||
連續的最弱的拓撲。此外,這個自然拓撲和
向量空間的線性結構相容,因為:
向量加法:+在此拓撲下是連續的,這可以由範數的三角不等式性質得出。
向量的數量乘法·在此拓撲下是連續的,這也可由範數的線性性和三角不等式性質得出。
對於半賦范向量空間,可以定義類似的函式,這時E成為一個半度量空間(弱於度量空間)。在其中我們也可以定義
連續和
收斂等概念。更抽象地說,每個半賦范向量空間都是一個
拓撲空間,其拓撲結構由它的半範數
誘導。
在賦范向量空間中,
完備的賦范向量空間特別重要,稱為
巴拿赫空間。每個賦范向量空間都是一個巴拿赫空間的
稠密子空間,這個巴拿赫空間由此賦范向量空間唯一確定,稱為它的
完備空間。
在拓撲的角度來說,有限維的向量空間上的任意兩個範數都是等價的,即它們誘導出相同的拓撲結構(儘管由它們各自定義的度量空間並不相同)。由於歐幾里得空間是完備的,我們可以推出每個有限維的賦范向量空間都是巴拿赫空間。實際上對自然拓撲來說,任意有限維的賦范向量空間都
同胚於歐幾里得空間
R。
一個賦范向量空間被稱為局部緊緻的,如果單位球是
緊集。由
里斯引理可知,一個賦范向量空間局部緊緻若且唯若它的維數有限。實際上,這個定理證明了對任意的
拓撲空間(不一定是由範數誘導的度量空間)都有這個結論。
線性變換和對偶空間
在賦范向量空間之間的
線性變換中,最重要的是連續線性變換,賦范向量空間和連續線性變換一起構成一個
範疇。
範數自身,作為函式,是連續的。任意兩個有限維的賦范向量空間之間的線性變換也都是連續的。
兩個賦范向量空間之間的一個等距變換
f是指使得對任意向量
v都有||
f(
v)|| = ||
v|| 的線性變換。保距變換總是連續的
單射。如果兩個賦范向量空間之間的一個等距變換是
滿射,那么稱其為一個
等距同構。兩個保距同構的賦范向量空間在拓撲的意義上可以說是相等的(擁有相同的性質;在一者中成立的命題,在另一者中也成立)。
對於在
域K上的賦范向量空間(E,||·||),我們可以考慮它關於||·||的
對偶空間E,也就是所有從E射到K的連續線性變換(一般稱為“
函子”)構成的空間。對於一個函子
,定義它的範數是
的
上確界,其中v是E中範數為 1 的所有向量。由於函子是連續的,這個上確界存在。這樣我們就將E定義成為一個賦范向量空間。 關於賦范向量空間上的連續線性函子有哈恩-巴拿赫定理。
商空間
很多賦范向量空間(特別是
巴拿赫空間)的定義涉及到空間上定義的半範數。賦范向量空間可以定義為一個空間關於半範數為零的元素的
商空間。比如說,對於L空間的定義,考慮所有函式組成的空間上的函式:
是一個半範數,它對所有能使式子右邊勒貝格可積的函式有定義。然而,對於任意定義在
勒貝格測度為 0 的支撐上的函式,其半範數皆為 0 。在“除掉”這些函式(將它們歸為 0 函式的等價類)之後,得到的商空間就是一個賦范向量空間:
LP空間。
空間的直積
給定n個半賦范向量空間(Ei,qi) ,我們可以定義它們的直積空間X為:
數量乘法定義為:
這是X上的一個半範數。q是範數若且唯若q
i都是範數。
對大於 1 的p,q也可以定義為:
這些半範數都是等價的。通過泛代數的結論可以證明,任意的有限維半賦范向量空間都可以表示成一個賦范向量空間和一個有平凡的半範數的半賦范向量空間的直積空間。因此,半賦范向量空間的比較有趣或“反常”的例子都是無限維的。
參見
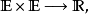
 ,定義它的範數是
,定義它的範數是 的上確界,其中v是E中範數為 1 的所有向量。由於函子是連續的,這個上確界存在。這樣我們就將E定義成為一個賦范向量空間。 關於賦范向量空間上的連續線性函子有哈恩-巴拿赫定理。
的上確界,其中v是E中範數為 1 的所有向量。由於函子是連續的,這個上確界存在。這樣我們就將E定義成為一個賦范向量空間。 關於賦范向量空間上的連續線性函子有哈恩-巴拿赫定理。