基本介紹
發展史
定義

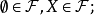




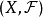


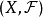


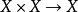
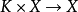

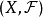
舉例
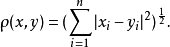
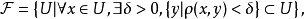
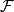

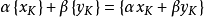

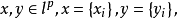
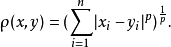
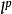
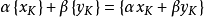
拓展
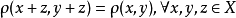
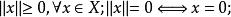
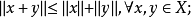
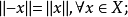
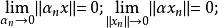
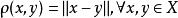

拓撲向量空間一般指本詞條

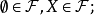




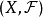


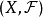


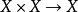
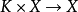

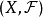
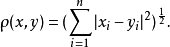
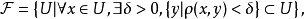
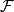

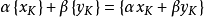

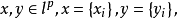
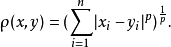
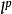
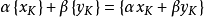
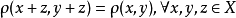
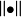
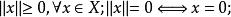
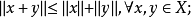
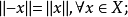
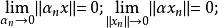
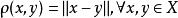
《拓撲學教程拓撲空間和距離空間、數值函式、拓撲向量空間》是2009年高等教育出版社出版的圖書,作者是G.肖蓋。...
為了更抽象地說,每個半規範向量空間是一個拓撲向量空間,因此承載了由半規範引起的拓撲結構。特別感興趣的是稱為Banach空間的完整規範空間。每個規範向量空間V坐在...
度量線性空間(metric linear space)是一類定義了距離的線性空間。設E是線性空間,又是度量空間,ρ是E上的距離,且E按ρ導出的拓撲成為拓撲線性空間,則稱E為度量...
它們有時叫做勒貝格空間,以昂利·勒貝格命名(Dunford & Schwartz 1958,III.3),儘管依據Bourbaki (1987)它們是Riesz (1910)首先介入。在泛函分析和拓撲向量空間中,...
一個拓撲向量空間的對偶空間是指由這個向量空間上的所有的連續線性泛函構成的泛函空間。對某個大於1的實數p,設q是滿足 的唯一實數,則空間Lp(S,μ)的對偶空間Lp...
初拓撲,在一般拓撲學與數學的相關領域中,給定集合X與集合X上的一族函式,其初拓撲(theinitialtopology)是使得這一族函式連續的最粗的拓撲。拓撲子空間與乘積空間都...
核型空間(nuclear space)是一類局部凸空間。局部凸空間是最重要的一類拓撲線性空間。設E是拓撲線性空間,如果E中存在由均衡凸集組成的零元的鄰域基,就稱E是局部凸...
《法蘭西數學精品譯叢·拓撲學教程:拓撲空間和距離空間、數值函式、拓撲向量空間(第2版)》中的基本概念幾乎都在其一般形式下來介紹,並通過例子來說明所選擇定義的...
代數拓撲(Algebraic topology)是使用抽象代數的工具來研究拓撲空間的數學分支。賦以拓撲的集合叫拓撲空間。拓撲基[topologique (base)]設E為拓撲向量空間,則E的任一...
在數學中, Lp空間是由p次可積函式組成的空間;對應的lp空間是由 p次可和序列組成的空間。在泛函分析和拓撲向量空間中,他們構成了Banach空間一類重要的例子。...
在數學裡,尤其是在泛函分析之中,巴拿赫空間是一個完備賦范向量空間。更精確地說,巴拿赫空間是一個具有範數並對此範數完備的向量空間。...
自反局部凸空間(reflexive locally convex space)屬於一類局部凸空間,也是屬於具有拓撲結構的線性空間。局部凸空間E為自反的充要條件是E為半自反的且是擬桶型的。...
