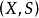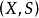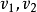勒貝格分解定理(Lebesgue decomposition theorem)是關於σ有限廣義測度分解為絕對連續部分和奇異部分之和的重要定理,是有界變差函式的勒貝格分解定理的推廣。設(Ω,F,μ)是σ有限測度空間,若γ是(Ω,F)上的σ有限測度,則γ可分解為兩個σ有限測度γs和γc之和:γ=γs+γc,使得γs⊥μ,γc≪μ(γs關於μ是奇異的,γc關於μ是絕對連續的)。γ的上述分解是惟一的。
基本介紹
- 中文名:勒貝格分解定理
- 外文名:Lebesgue decomposition theorem
- 所屬學科:數學
- 所屬問題:測度論(測度和積分)
基本介紹,定理的證明,
基本介紹
設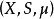 是
是 有限測度空間,又
有限測度空間,又 是
是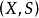 上的有限測度,則存在
上的有限測度,則存在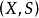 上的有限測度
上的有限測度 ,使
,使
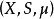


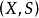
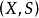

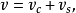


定理的證明
引理1 設 分別是可測空間
分別是可測空間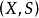 上的測度和有限廣義測度,則v對
上的測度和有限廣義測度,則v對 絕對連續且v是
絕對連續且v是 奇異的充要條件是:對每一
奇異的充要條件是:對每一 。(三個引理的證明請參考相應書籍)。
。(三個引理的證明請參考相應書籍)。

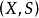



證明:充分性顯然。往證必要性,因v是 奇異的,故有
奇異的,故有 ,且對每一
,且對每一 ,有
,有 ,因對一切
,因對一切 ,均有
,均有 ,並注意
,並注意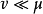 ,故對每一
,故對每一 ,
, ,從而
,從而






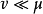




1) 若 和
和 ,則
,則 ;
;



2) 若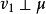 和
和 ,則
,則 。
。
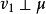


證明:1)是顯然的。往證2)。因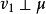 和
和 ,故有
,故有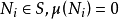 ,且對每一
,且對每一 有
有 ,令
,令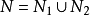 ,那么
,那么
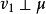

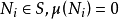


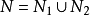





引理3 設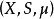 是
是 有限測度空間,又v是
有限測度空間,又v是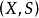 上的有限測度,則存在非負可測實函式
上的有限測度,則存在非負可測實函式 及
及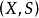 上的有限測度
上的有限測度 ,使得
,使得
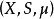

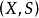

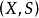


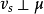

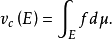
(第三個引理的證明請參考相應書籍)。
勒貝格分解定理的證明 由引理3知,存在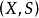 上的有限測度
上的有限測度 ,使
,使 且
且 ,
, 。下面我們證明上述分解式是唯一的。設v又可分解為
。下面我們證明上述分解式是唯一的。設v又可分解為 ,其中
,其中 是
是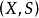 上的有限測度,且
上的有限測度,且 ,
, ;那么從
;那么從