若在區間(a,b)中,函式f(x)能夠表成Φ(x)一Ψ(x)的形狀,而Φ與Ψ都是非減有界函式,則稱f(x)在(a,b)中是有界變差的.易見兩有界變差函式的和、差與積也都是有界變差的.
基本介紹
- 中文名:有界變差函式
- 外文名:bounded variation
- 含義:表為兩個單調增函式之差的實值
- 類別:常用的函式類
定義
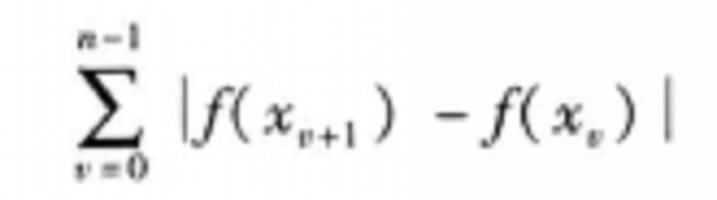
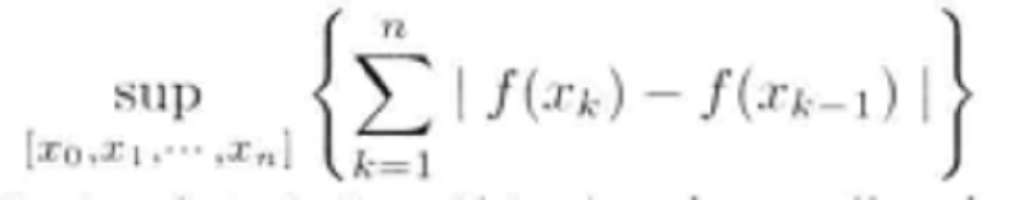
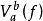
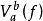
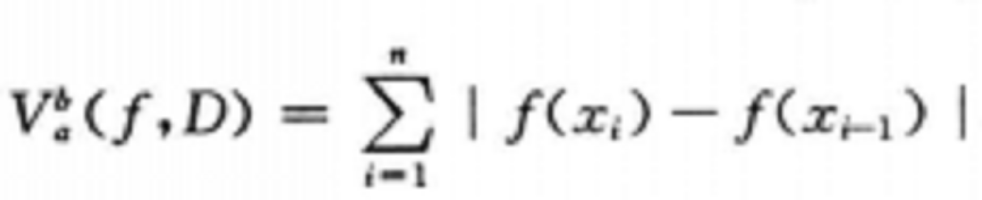
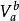
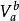
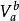
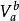
性質
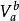
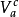
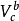
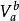
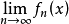
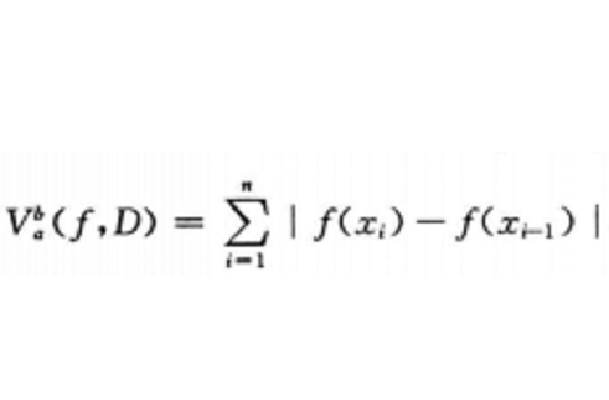
若在區間(a,b)中,函式f(x)能夠表成Φ(x)一Ψ(x)的形狀,而Φ與Ψ都是非減有界函式,則稱f(x)在(a,b)中是有界變差的.易見兩有界變差函式的和、差與積也都是有界變差的.
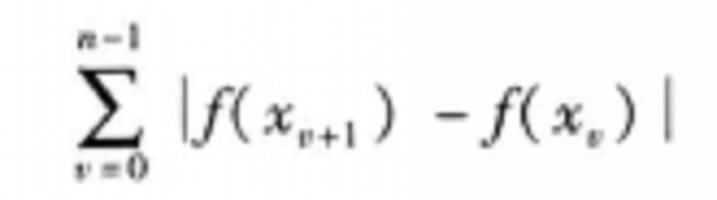
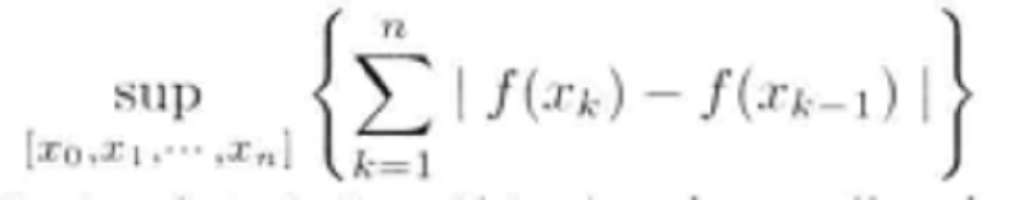
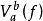
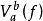
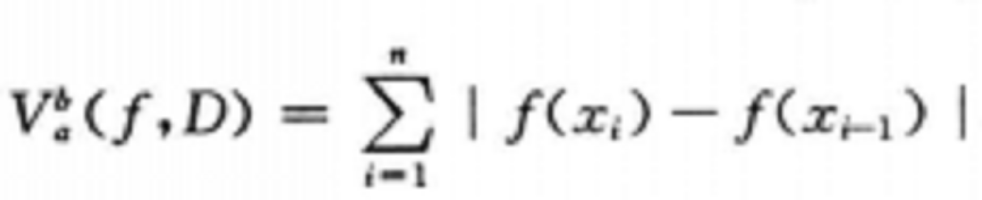
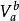
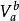
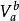
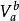
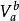
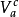
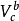
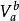
若在區間(a,b)中,函式f(x)能夠表成Φ(x)一Ψ(x)的形狀,而Φ與Ψ都是非減有界函式,則稱f(x)在(a,b)中是有界變差的.易見兩有界變差函式的和、...
《實變函式》是2009年東南大學出版社出版的圖書,作者是張建平、丘京輝。本書在n維歐氏空間中建立Lebesgue測度和積分的理論,突出體現實變函式的基本思想。...
6.2 有界變差函式6.3 絕對連續函式6.4 抽象測度與Radon-Nikodym定理習題6附錄A Stieltjes積分簡介附錄B Fourier級數的點態收斂定理附錄C 習題選解...
6.1 單調函式的可微性6.2 有界變差函式6.3 絕對連續函式與不定積分習題六第七章 L空間附錄I 等價關係 半序集與Zorn引理附錄II 實數集與極限論...
作者:周性偉 本書是作者在多年教學經驗的基礎上撰寫的一部實變函式教材,第二版在第一版使用9年的基礎上作了修訂。本書內容包括:集合與實數集、Lebesgue測度、可...
第1章導言,簡單介紹勒貝格測度與勒貝格積分的起源及其基本理念;第2~6章分別為集合、n維歐氏空間、測度論、可測函式、積分論;第7章有界變差函式與絕對連續函式,...
《實變函式解題指南》是2007年北京大學出版社出版的圖書,作者是周民強。 [1] 本書是實變函式課程的學習輔導用書,其內容是在作者編寫的普通高等教育“九五”教育部...
第一節 單調函式的可微性主要內容疑難分析典型例題第二節 有界變差函式主要內容疑難分析典型例題第三節 不定積分的微分主要內容疑難分析...
2.單調函式的可微性 3.有界變差函式 4.不定積分 5.斯蒂爾切斯(Stieltjes)積分 6.勒貝格-斯蒂爾切斯測度與積分 第六章習題 第二篇 泛函分析 第七章 度量空間...
《實變函式簡明教程》是華中理工大學出版社出版的圖書。本書主要介紹了集合的...§4.1 連續函式§4.2 單調函式與有界變差函式§4.3 絕對連續函式...
廣義有界變差函式是集上的有界變差函式的推廣。若f(x)在每個En上是有界變差的,則稱f(x)是E上的廣義有界變差函式。...
《實變函式(第二版)》是2014年東南大學出版社出版的圖書,作者是張建平,丘京輝...6 2有界變差函式1206 3不定積分的微分1236 4絕對連續函式126...
§3.1 連續函式與單調函式*§3.2 有界變差函式與絕對連續函式§3.3 簡單函式§3.4 可測函式的概念與性質§3.5 可測函式的逼近...
3.絕對連續函式一定是有界變差函式,但有界變差函式未必是絕對連續函式。4.若f(x)在[a,b]上絕對連續,且f′(x)=0 a.e.於[a,b],則f(x)為一常數。...
而且引入了可數可加集合函式的概念(定義于勒貝格可測集類上),指出這些函式是定義在集合類上的有界變差函式.正是因為對於有界變差與可加性概念之間聯繫的考察,...
黑利選擇定理是有界變差函式的一個重要性質。設{fα(x)|α∈Γ}是[a,b]上一族(無限個)一致有界的有界變差函式,它們的全變差也有界,則存在{fα(x)|...
勒貝格分解定理(Lebesgue decomposition theorem)是關於σ有限廣義測度分解為絕對連續部分和奇異部分之和的重要定理,是有界變差函式的勒貝格分解定理的推廣。設(Ω,F,...
本書匯集了實分析中的大量反例,主要內容有集合、函式、微分、Riemann積分、無窮級數、一致收斂、Lebesgue測度和Lebesgue積分、有界變差函式和絕對連續函式。對平麵點集...
,可以構造有界變差函式 ,使得無論連續函式 是什麼,都有 ”在量子力學的數學處理中,這個定理可以視為流行的狄拉克符號記法的根據。當定理成立時,每個右括弧 ...
本書講述能量泛函正則化模型在圖像恢復中的套用,主要內容包括圖像恢復基本原理,能量泛函變分原理,有界變差函式原理,凸分析基本原理,能量泛函解的存在性、唯一性和...
